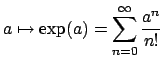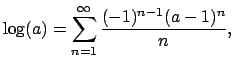Let  be a field with a non-archimedean valuation
be a field with a non-archimedean valuation
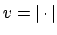 .
Recall that the set of
.
Recall that the set of  with
with
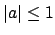 forms a ring
forms a ring
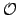 , the ring of integers for
, the ring of integers for 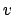 . The set of
. The set of 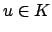 with
with
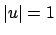 are a group
are a group 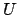 under multiplication, the group of units
for
under multiplication, the group of units
for 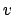 . Finally, the set of
. Finally, the set of 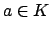 with
with
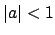 is a maximal
ideal
is a maximal
ideal
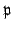 , so the quotient ring
, so the quotient ring
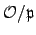 is a field. In this section
we consider the case when
is a field. In this section
we consider the case when
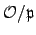 is a finite field of order a prime
power
is a finite field of order a prime
power 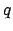 . For example,
. For example,  could be
could be
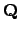 and
and
 could be a
could be a
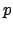 -adic valuation, or
-adic valuation, or  could be a number field and
could be a number field and
 could be the valuation corresponding to a maximal ideal of the ring of
integers. Among other things, we will discuss in more depth the
topological and measure-theoretic nature of the completion of
could be the valuation corresponding to a maximal ideal of the ring of
integers. Among other things, we will discuss in more depth the
topological and measure-theoretic nature of the completion of  at
at
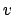 .
.
Suppose further for the rest of this section that
 is
discrete. Then by Lemma 15.2.8, the ideal
is
discrete. Then by Lemma 15.2.8, the ideal
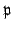 is a principal ideal
is a principal ideal 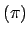 , say, and every
, say, and every 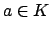 is of the form
is of the form
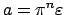 , where
, where
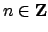 and
and
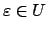 is a unit. We call
is a unit. We call
the ord of 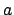 at
at 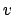 . (Some authors, including me (!) also call
this integer the of
. (Some authors, including me (!) also call
this integer the of 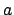 with respect to
with respect to 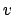 .) If
.) If
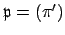 , then
, then 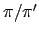 is a unit, and conversely, so
is a unit, and conversely, so 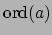 is independent of the choice of
is independent of the choice of  .
.
Let 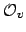 and
and
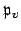 be defined with respect to the completion
be defined with respect to the completion 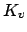 of
of  at
at 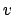 .
.
Lemma 17.1.1
There is a natural isomorphism
and
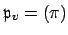 as an
as an 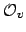 -ideal.
-ideal.
Proof.
We may view
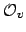
as the set of equivalence classes of Cauchy
sequences
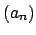
in

such that
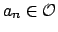
for
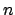
sufficiently
large. For any
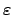
, given such a sequence
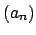
, there is
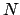
such that for
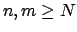
, we have
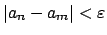
. In
particular, we can choose
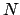
such that
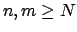
implies that
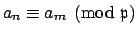
. Let
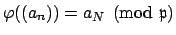
, which is
well-defined. The map
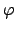
is surjective because the constant
sequences are in
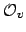
. Its kernel is the set of Cauchy sequences
whose elements are eventually all in
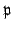
, which is exactly
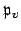
.
This proves the first part of the lemma. The second part is true
because any element of
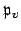
is a sequence all of whose terms are
eventually in
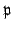
, hence all a multiple of
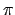
(we can set to
0
a finite number of terms of the sequence without changing the
equivalence class of the sequence).

Assume for the rest of this section that  is complete with
respect to
is complete with
respect to
 .
.
By (17.1.1) is meant the limit of the Cauchy sequence
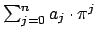 as
as
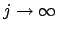 .
.
Proof.
There is a uniquely defined
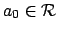
such that
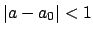
.
Then
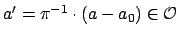
. Now define
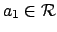
by
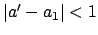
. And so on.

Example 17.1.3
Suppose
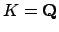
and
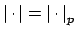
is the
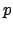
-adic valuation,
for some prime
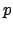
. We can take
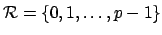
.
The lemma asserts that
Notice that
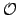
is uncountable since there are
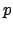
choices for each
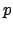
-adic ``digit''. We can do arithmetic with
elements of
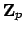
, which can be thought of ``backwards'' as numbers
in base
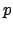
. For example, with
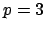
we have
| |
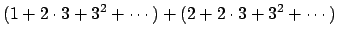 |
|
| |
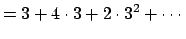 not in canonical form not in canonical form |
|
| |
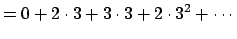 still not canonical still not canonical |
|
| |
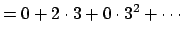 |
|
Basic arithmetic with the 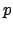 -adics in is really weird (even
weirder than it was a year ago... There are presumably efficiency
advantages to using the formalization, and it's supposed to be
better for working with extension fields. But I can't get it to do
even the calculation below in a way that is clear.) In PARI (gp) the
-adics in is really weird (even
weirder than it was a year ago... There are presumably efficiency
advantages to using the formalization, and it's supposed to be
better for working with extension fields. But I can't get it to do
even the calculation below in a way that is clear.) In PARI (gp) the
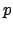 -adics work as expected:
-adics work as expected:
? a = 1 + 2*3 + 3^2 + O(3^3);
? b = 2 + 2*3 + 3^2 + O(3^3);
? a+b
%3 = 2*3 + O(3^3)
? sqrt(1+2*3+O(3^20))
%5 = 1 + 3 + 3^2 + 2*3^4 + 2*3^7 + 3^8 + 3^9 + 2*3^10 + 2*3^12
+ 2*3^13 + 2*3^14 + 3^15 + 2*3^17 + 3^18 + 2*3^19 + O(3^20)
? 1/sqrt(1+2*3+O(3^20))
%6 = 1 + 2*3 + 2*3^2 + 2*3^7 + 2*3^10 + 2*3^11 + 2*3^12 + 2*3^13
+ 2*3^14 + 3^15 + 2*3^16 + 2*3^17 + 3^18 + 3^19 + O(3^20)
Theorem 17.1.4
Under the conditions of the preceding lemma, 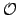 is compact with
respect to the
is compact with
respect to the
 -topology.
-topology.
Proof.
Let
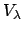
, for
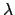
running through some index set
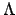
, be some family of open sets that cover
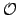
. We must
show that there is a finite subcover. We suppose not.
Let
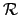 be a set of representatives for
be a set of representatives for
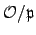 . Then
. Then 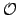 is the
union of the finite number of cosets
is the
union of the finite number of cosets 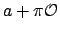 , for
, for
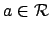 .
Hence for at lest one
.
Hence for at lest one
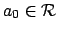 the set
the set
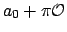 is not covered by finitely many of the
is not covered by finitely many of the 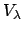 . Then similarly
there is an
. Then similarly
there is an
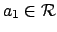 such that
such that
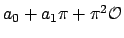 is not
finitely covered. And so on. Let
is not
finitely covered. And so on. Let
Then
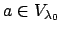
for some
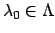
. Since
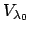
is an open set,
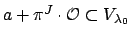
for some
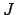
(since those are exactly the open balls
that form a basis for the topology). This is a contradiction because
we constructed
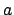
so that none of the sets
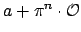
, for
each
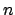
, are not covered by any finite subset of the
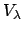
.

Definition 17.1.5 (Locally compact)
A topological space
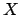
is
at a point
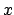
if
there is some compact subset
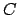
of
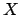
that contains a neighborhood
of
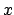
. The space
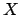
is locally compact if it is locally compact
at each point in
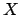
.
Proof.
If
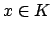
, then
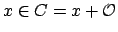
, and
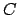
is a compact subset of

by Theorem
17.1.4. Also
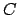
contains the neighborhood
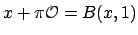
of
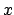
. Thus

is locally compact at
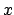
.

Remark 17.1.7
The converse is also true. If

is locally compact with respect to
a non-archimedean valuation

, then
 is complete,
is complete,
- the residue field is finite, and
- the valuation is discrete.
For there is a compact neighbourhood
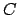
of
0.
Let
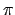
be any nonzero with
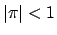
.
Then
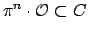
for sufficiently large
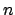
, so
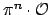
is
compact, being closed. Hence
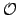
is compact. Since

is a
metric,
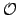
is sequentially compact, i.e., every fundamental sequence
in
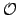
has a limit, which implies (1). Let
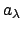
(for
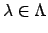
) be a set of representatives in
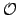
of
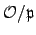
.
Then
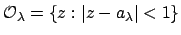
is an open
covering of
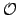
. Thus (2) holds since
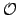
is compact. Finally,
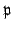
is compact, being a closed subset of
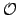
. Let
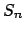
be the set
of
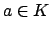
with
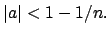
Then
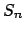
(for
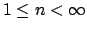
)
is an open covering of
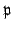
, so
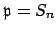
for some
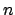
, i.e., (3) is
true.
If we allow
 to be archimedean the only further
possibilities are
to be archimedean the only further
possibilities are
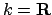 and
and
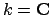 with
with
 equivalent to the
usual absolute value.
equivalent to the
usual absolute value.
We denote by 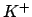 the commutative topological group whose points are
the elements of
the commutative topological group whose points are
the elements of  , whose group law is addition and whose topology is
that induced by
, whose group law is addition and whose topology is
that induced by
 . General theory tells us that there is an
invariant Haar measure defined on
. General theory tells us that there is an
invariant Haar measure defined on 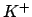 and that this
measure is unique up to a multiplicative constant.
and that this
measure is unique up to a multiplicative constant.
Definition 17.1.8 (Haar Measure)
A
on a locally compact topological group
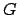
is a translation invariant measure such that every open
set can be covered by open sets with finite measure.
Lemma 17.1.9
Haar measure of any compact subset 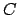 of
of 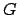 is finite.
is finite.
Proof.
The whole group
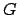
is open, so there is a covering
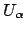
of
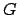
by open sets each of which has finite measure.
Since
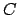
is compact, there is a finite subset of the
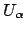
that covers
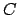
. The measure of
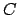
is at most the sum of
the measures of these finitely many
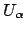
, hence finite.

Remark 17.1.10
Usually one defined Haar measure to be a translation invariant
measure such that the measure of compact sets is finite. Because of
local compactness, this definition is equivalent to
Definition
17.1.8. We take this alternative viewpoint
because Haar measure is constructed naturally on the topological
groups we will consider by defining the measure on each member of a
basis of open sets for the topology.
We now deduce what any such measure 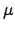 on
on 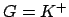 must be. Since
must be. Since
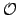 is compact (Theorem 17.1.4), the measure of
is compact (Theorem 17.1.4), the measure of 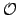 is
finite. Since
is
finite. Since 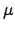 is translation invariant,
is translation invariant,
is independent of 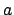 . Further,
. Further,
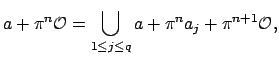
(disjoint union)
where 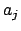 (for
(for
 ) is a set of representatives of
) is a set of representatives of
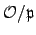 . Hence
If we normalize
. Hence
If we normalize 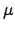 by putting
we have
by putting
we have 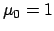 , hence
, hence 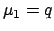 , and in general
, and in general
Conversely, without the theory of Haar measure, we could define
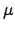 to be the necessarily unique measure on
to be the necessarily unique measure on 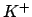 such that
such that
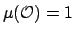 that is translation invariant. This would have to be the
that is translation invariant. This would have to be the
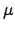 we just found above.
we just found above.
Everything so far in this section has depended not on the valuation
 but only on its equivalence class. The above
considerations now single out one valuation in the equivalence class
as particularly important.
but only on its equivalence class. The above
considerations now single out one valuation in the equivalence class
as particularly important.
Definition 17.1.11 (Normalized valuation)
Let

be a field equipped with a discrete valuation

and residue class field with
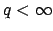
elements. We say that

is
if
where
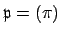
is the maximal ideal of
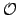
.
The following proposition makes clear why this is the best choice of
normalization.
Proof.
Since
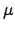
is translation invariant,
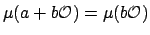
.
Write
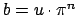
, where
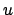
is a unit. Then since
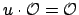
, we have
Here we have
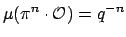
by the discussion
before Definition
17.1.11.

We can express the result of the theorem in a more suggestive way.
Let 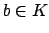 with
with 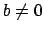 , and let
, and let 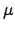 be a Haar measure on
be a Haar measure on 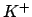 (not necessarily normalized as in the theorem). Then we can define a
new Haar measure
(not necessarily normalized as in the theorem). Then we can define a
new Haar measure 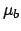 on
on 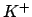 by putting
by putting
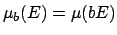 for
for
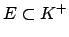 . But Haar measure is unique up to a multiplicative
constant and so
. But Haar measure is unique up to a multiplicative
constant and so
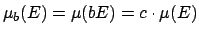 for all
measurable sets
for all
measurable sets 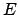 , where the factor
, where the factor 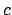 depends only on
depends only on 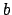 .
Putting
.
Putting 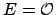 , shows that the theorem implies that
, shows that the theorem implies that 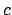 is just
is just
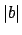 , when
, when
 is the normalized valuation.
is the normalized valuation.
Remark 17.1.14
The theory of locally compact topological groups leads to the
consideration of the dual (character) group of
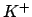
. It turns out
that it is isomorphic to
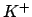
. We do not need this fact for class
field theory, so do not prove it here. For a proof and applications
see Tate's thesis or Lang's
Algebraic Numbers, and for
generalizations see Weil's
Adeles and Algebraic Groups and
Godement's Bourbaki seminars 171 and 176. The determination of the
character group of
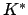
is local class field theory.
The set of nonzero elements of  is a group
is a group 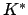 under
multiplication. Multiplication and inverses are continuous with
respect to the topology induced on
under
multiplication. Multiplication and inverses are continuous with
respect to the topology induced on 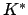 as a subset of
as a subset of  , so
, so 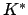 is a topological group with this topology. We have
is a topological group with this topology. We have
where 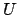 is the group of units of
is the group of units of
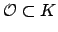 and
and 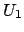 is
the group of
is
the group of 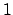 -units, i.e., those units
-units, i.e., those units
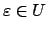 with
with
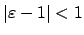 , so
The set
, so
The set 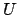 is the open ball about 0 of
radius
is the open ball about 0 of
radius 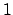 , so is open, and because the metric is nonarchimedean
, so is open, and because the metric is nonarchimedean 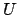 is also closed. Likewise,
is also closed. Likewise, 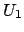 is both open and closed.
is both open and closed.
The quotient
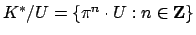 is isomorphic to the additive group
is isomorphic to the additive group
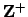 of integers with the discrete topology, where the map is
of integers with the discrete topology, where the map is
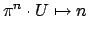
for
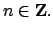
The quotient
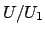 is isomorphic to the multiplicative group
is isomorphic to the multiplicative group
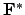 of the
nonzero elements of the residue class field, where the finite gorup
of the
nonzero elements of the residue class field, where the finite gorup
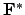 has the discrete topology.
Note that
has the discrete topology.
Note that
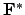 is cyclic
of order
is cyclic
of order 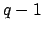 , and Hensel's lemma implies that
, and Hensel's lemma implies that 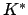 contains a
primitive
contains a
primitive 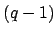 th root of unity
th root of unity 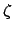 . Thus
. Thus 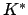 has
the following structure:
has
the following structure:
(How to apply Hensel's lemma: Let
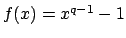 and let
and let
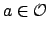 be such that
be such that
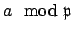 generates
generates 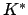 . Then
. Then
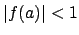 and
and
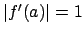 . By Hensel's lemma there is a
. By Hensel's lemma there is a
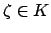 such that
such that
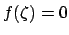 and
and
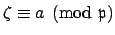 .)
.)
Since 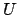 is compact and the cosets of
is compact and the cosets of 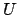 cover
cover  , we see that
, we see that
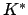 is locally compact.
is locally compact.
Lemma 17.1.15
The additive Haar measure 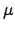 on
on 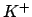 ,
when restricted to
,
when restricted to 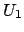 gives a measure on
gives a measure on 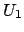 that is also
invariant under multiplication, so gives a Haar measure on
that is also
invariant under multiplication, so gives a Haar measure on 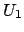 .
.
Proof.
It suffices to show that
for any
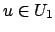
and
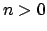
.
Write
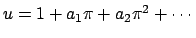
.
We have
which is an additive translate of
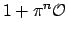
, hence has the
same measure.

Thus 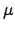 gives a Haar measure on
gives a Haar measure on 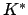 by translating
by translating 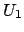 around
to cover
around
to cover 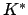 .
.
Lemma 17.1.16
The topological spaces 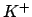 and
and 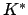 are totally disconnected (the
only connected sets are points).
are totally disconnected (the
only connected sets are points).
Proof.
The proof is the same as that of
Proposition
16.2.13. The point is that the
non-archimedean triangle inequality forces the complement an open
disc to be open, hence any set with at least two distinct elements
``falls apart'' into a disjoint union of two disjoint open subsets.

Remark 17.1.17
Note that
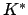
and
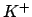
are locally isomorphic if

has
characteristic
0. We have the exponential map
defined for all sufficiently small
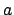
with its inverse
which is defined for all
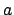
sufficiently close to
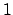
.
William Stein
2004-05-06
![]() is
discrete. Then by Lemma 15.2.8, the ideal
is
discrete. Then by Lemma 15.2.8, the ideal
![]() is a principal ideal
is a principal ideal ![]() , say, and every
, say, and every ![]() is of the form
is of the form
![]() , where
, where
![]() and
and
![]() is a unit. We call
is a unit. We call
![]() and
and
![]() be defined with respect to the completion
be defined with respect to the completion ![]() of
of ![]() at
at ![]() .
.
![]() is complete with
respect to
is complete with
respect to
![]() .
.
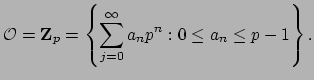
![]() -adics in is really weird (even
weirder than it was a year ago... There are presumably efficiency
advantages to using the formalization, and it's supposed to be
better for working with extension fields. But I can't get it to do
even the calculation below in a way that is clear.) In PARI (gp) the
-adics in is really weird (even
weirder than it was a year ago... There are presumably efficiency
advantages to using the formalization, and it's supposed to be
better for working with extension fields. But I can't get it to do
even the calculation below in a way that is clear.) In PARI (gp) the
![]() -adics work as expected:
-adics work as expected:
![]() be a set of representatives for
be a set of representatives for
![]() . Then
. Then ![]() is the
union of the finite number of cosets
is the
union of the finite number of cosets ![]() , for
, for
![]() .
Hence for at lest one
.
Hence for at lest one
![]() the set
the set
![]() is not covered by finitely many of the
is not covered by finitely many of the ![]() . Then similarly
there is an
. Then similarly
there is an
![]() such that
such that
![]() is not
finitely covered. And so on. Let
is not
finitely covered. And so on. Let
![]() to be archimedean the only further
possibilities are
to be archimedean the only further
possibilities are
![]() and
and
![]() with
with
![]() equivalent to the
usual absolute value.
equivalent to the
usual absolute value.![]() the commutative topological group whose points are
the elements of
the commutative topological group whose points are
the elements of ![]() , whose group law is addition and whose topology is
that induced by
, whose group law is addition and whose topology is
that induced by
![]() . General theory tells us that there is an
invariant Haar measure defined on
. General theory tells us that there is an
invariant Haar measure defined on ![]() and that this
measure is unique up to a multiplicative constant.
and that this
measure is unique up to a multiplicative constant.
![]() on
on ![]() must be. Since
must be. Since
![]() is compact (Theorem 17.1.4), the measure of
is compact (Theorem 17.1.4), the measure of ![]() is
finite. Since
is
finite. Since ![]() is translation invariant,
is translation invariant,
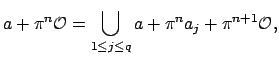 (disjoint union)
(disjoint union)
![]() to be the necessarily unique measure on
to be the necessarily unique measure on ![]() such that
such that
![]() that is translation invariant. This would have to be the
that is translation invariant. This would have to be the
![]() we just found above.
we just found above.
![]() but only on its equivalence class. The above
considerations now single out one valuation in the equivalence class
as particularly important.
but only on its equivalence class. The above
considerations now single out one valuation in the equivalence class
as particularly important.
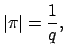
![]() . Then the
. Then the ![]() -adic valuation on
-adic valuation on
![]() extends uniquely to one on
extends uniquely to one on ![]() such that
such that
![]() . Since
. Since
![]() for
for ![]() , this valuation is not normalized. (Note that
the ord of
, this valuation is not normalized. (Note that
the ord of
![]() is
is ![]() .)
The normalized valuation is
.)
The normalized valuation is
![]() . Note that
. Note that
![]() , or
, or
![]() instead of
instead of ![]() .
.
![]() where
where ![]() has not root mod
has not root mod ![]() . Then the residue class field
degree is
. Then the residue class field
degree is ![]() , and the normalized valuation must
satisfy
, and the normalized valuation must
satisfy
![]() .
.![]() with
with ![]() , and let
, and let ![]() be a Haar measure on
be a Haar measure on ![]() (not necessarily normalized as in the theorem). Then we can define a
new Haar measure
(not necessarily normalized as in the theorem). Then we can define a
new Haar measure ![]() on
on ![]() by putting
by putting
![]() for
for
![]() . But Haar measure is unique up to a multiplicative
constant and so
. But Haar measure is unique up to a multiplicative
constant and so
![]() for all
measurable sets
for all
measurable sets ![]() , where the factor
, where the factor ![]() depends only on
depends only on ![]() .
Putting
.
Putting ![]() , shows that the theorem implies that
, shows that the theorem implies that ![]() is just
is just
![]() , when
, when
![]() is the normalized valuation.
is the normalized valuation.
![]() is a group
is a group ![]() under
multiplication. Multiplication and inverses are continuous with
respect to the topology induced on
under
multiplication. Multiplication and inverses are continuous with
respect to the topology induced on ![]() as a subset of
as a subset of ![]() , so
, so ![]() is a topological group with this topology. We have
is a topological group with this topology. We have
![]() is isomorphic to the additive group
is isomorphic to the additive group
![]() of integers with the discrete topology, where the map is
of integers with the discrete topology, where the map is
![]() is isomorphic to the multiplicative group
is isomorphic to the multiplicative group
![]() of the
nonzero elements of the residue class field, where the finite gorup
of the
nonzero elements of the residue class field, where the finite gorup
![]() has the discrete topology.
Note that
has the discrete topology.
Note that
![]() is cyclic
of order
is cyclic
of order ![]() , and Hensel's lemma implies that
, and Hensel's lemma implies that ![]() contains a
primitive
contains a
primitive ![]() th root of unity
th root of unity ![]() . Thus
. Thus ![]() has
the following structure:
has
the following structure:
![]() is compact and the cosets of
is compact and the cosets of ![]() cover
cover ![]() , we see that
, we see that
![]() is locally compact.
is locally compact.