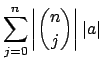We define two important properties of valuations, both of which
apply to equivalence classes of valuations (i.e., the property
holds for
 if and only if it holds for a valuation
equivalent to
if and only if it holds for a valuation
equivalent to
 ).
).
Definition 15.2.1 (Discrete)
A valuation

is
if there is a
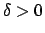
such that for any
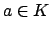
Thus the absolute values are bounded away from
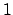
.
To say that
 is discrete is the same as saying
that the set
forms a discrete subgroup of the reals under addition (because
the elements of the group
is discrete is the same as saying
that the set
forms a discrete subgroup of the reals under addition (because
the elements of the group 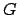 are bounded away from 0).
are bounded away from 0).
Proof.
Since
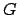
is discrete there is a positive
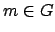
such that for any positive
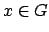
we have
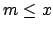
.
Suppose
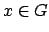
is an arbitrary positive element.
By subtracting off integer multiples of
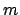
, we
find that there is a unique
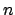
such that
Since
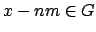
and
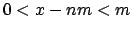
, it follows
that
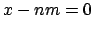
, so
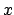
is a multiple of
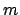
.

By Proposition 15.2.2, the set
of
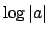 for nonzero
for nonzero 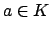 is free on one generator, so there
is a
is free on one generator, so there
is a 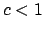 such that
such that
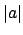 , for
, for 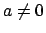 ,
runs precisely through the set
(Note: we can replace
,
runs precisely through the set
(Note: we can replace 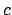 by
by 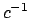 to see that we
can assume that
to see that we
can assume that 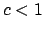 ).
).
Definition 15.2.3 (Order)
If
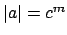
, we call
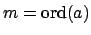
the
of
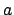
.
Axiom (2) of valuations
translates into
Definition 15.2.4 (Non-archimedean)
A valuation

is
if we can take
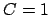
in Axiom (3), i.e., if
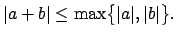 |
(15.3) |
If

is not non-archimedean then
it is
.
Note that if we can take 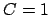 for
for
 then we can take
then we can take 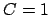 for any valuation equivalent to
for any valuation equivalent to
 .
To see that (15.2.1) is equivalent to Axiom (3) with
.
To see that (15.2.1) is equivalent to Axiom (3) with
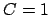 , suppose
, suppose
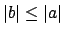 . Then
. Then
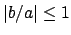 , so
Axiom (3) asserts that
, so
Axiom (3) asserts that
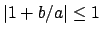 , which implies
that
, which implies
that
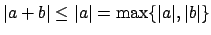 , and conversely.
, and conversely.
We note at once the following consequence:
Lemma 15.2.5
Suppose
 is a non-archimedean valuation.
If
is a non-archimedean valuation.
If 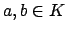 with
with 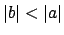 , then
, then
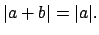
Proof.
Note that
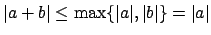
, which
is true even if
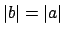
. Also,
where for the last equality we have used that
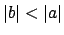
(if
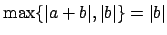
, then
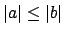
,
a contradiction).

Definition 15.2.6 (Ring of Integers)
Suppose

is a non-archimedean absolute
value on a field

. Then
is a ring called the
of

with respect to

.
Lemma 15.2.7
Two non-archimedean valuations
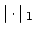 and
and
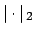 are equivalent if and only if they
give the same
are equivalent if and only if they
give the same 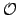 .
.
We will prove this modulo the claim (to
be proved later in Section 16.1) that
valuations are equivalent if (and only if) they induce the
same topology.
Proof.
Suppose suppose
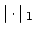
is equivalent to
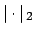
, so
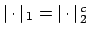
,
for some
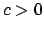
. Then
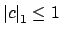
if and only if
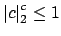
, i.e., if
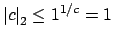
.
Thus
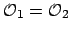
.
Conversely, suppose
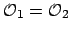 .
Then
.
Then
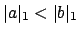 if and only if
if and only if
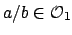 and
and
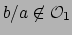 , so
, so
 |
(15.4) |
The topology induced by
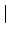
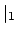
has as basis
of open neighborhoods the set of open balls
for
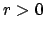
, and likewise for
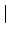
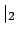
. Since
the absolute values
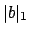
get arbitrarily close
to
0, the set
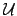
of open balls
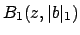
also
forms a basis of the topology induced
by
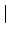
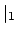
(and similarly for
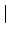
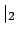
).
By (
15.2.2) we have
so the two topologies both have
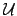
as
a basis, hence are equal. That equal topologies
imply equivalence of the corresponding valuations
will be proved in Section
16.1.

The set of 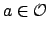 with
with 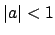 forms an ideal
forms an ideal
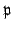 in
in 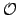 . The
ideal
. The
ideal
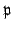 is maximal, since if
is maximal, since if 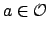 and
and
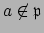 then
then
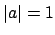 , so
, so
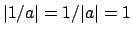 , hence
, hence 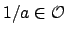 , so
, so 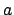 is a unit.
is a unit.
Lemma 15.2.8
A non-archimedean valuation
 is
discrete if and only if
is
discrete if and only if
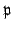 is a principal ideal.
is a principal ideal.
Proof.
First suppose that

is discrete.
Choose
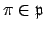
with
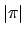
maximal, which
we can do since
so the discrete set
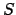
is bounded above.
Suppose
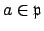
. Then
so
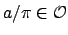
.
Thus
Conversely, suppose
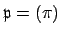 is principal. For any
is principal. For any
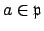 we have
we have 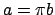 with
with 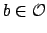 . Thus
. Thus
Thus
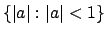
is bounded away from
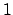
,
which is exactly the definition of discrete.

Example 15.2.9
For any prime
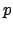
, define the
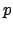
-adic valuation
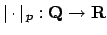
as follows. Write a nonzero
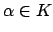
as
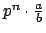
, where
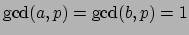
. Then
This valuation is both discrete and non-archimedean.
The ring
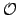
is the local ring
which has maximal ideal generated by
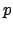
. Note that
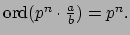
We will using the following lemma later (e.g., in
the proof of Corollary 16.2.4 and Theorem 15.3.2).
Lemma 15.2.10
A valuation
 is non-archimedean if and only if
is non-archimedean if and only if 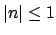 for all
for all  in the ring generated by
in the ring generated by  in
in  .
.
Note that we cannot identify the ring generated by 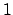 with
with
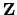 in general, because
in general, because  might have characteristic
might have characteristic 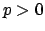 .
.
Proof.
If

is non-archimedean, then
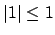
,
so by Axiom (3) with
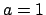
, we have
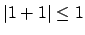
. By
induction it follows that
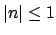
.
Conversely, suppose 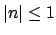 for all integer multiples
for all integer multiples 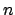 of
of 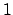 .
This condition is also true if we replace
.
This condition is also true if we replace
 by
any equivalent valuation, so replace
by
any equivalent valuation, so replace
 by
one with
by
one with 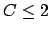 , so that the triangle inequality holds.
Suppose
, so that the triangle inequality holds.
Suppose 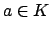 with
with 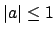 . Then
by the triangle inequality,
. Then
by the triangle inequality,
Now take
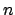
th roots of both sides to get
and take the limit as
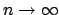
to see
that
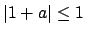
. This proves that one
can take
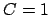
in Axiom (3), hence that

is non-archimedean.

William Stein
2004-05-06
![]()
![]() .
Then
.
Then
![]() if and only if
if and only if
![]() and
and
![]() , so
, so
![]() with
with ![]() forms an ideal
forms an ideal
![]() in
in ![]() . The
ideal
. The
ideal
![]() is maximal, since if
is maximal, since if ![]() and
and
![]() then
then
![]() , so
, so
![]() , hence
, hence ![]() , so
, so ![]() is a unit.
is a unit.
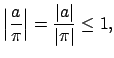
![]() is principal. For any
is principal. For any
![]() we have
we have ![]() with
with ![]() . Thus
. Thus
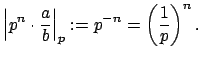
![]() for all integer multiples
for all integer multiples ![]() of
of ![]() .
This condition is also true if we replace
.
This condition is also true if we replace
![]() by
any equivalent valuation, so replace
by
any equivalent valuation, so replace
![]() by
one with
by
one with ![]() , so that the triangle inequality holds.
Suppose
, so that the triangle inequality holds.
Suppose ![]() with
with ![]() . Then
by the triangle inequality,
. Then
by the triangle inequality,