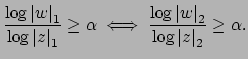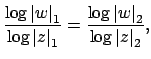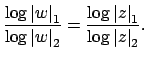A valuation satisfying the triangle inequality gives a metric for the
topology on defining the distance from 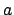 to
to 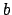 to be
to be
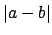 .
Assume for the rest of this section that we only consider valuations
that satisfy the triangle inequality.
.
Assume for the rest of this section that we only consider valuations
that satisfy the triangle inequality.
Proof.
It suffices to prove that if
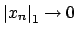
then
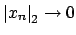
, since the proof of the
other implication is the same.
Let
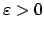
. The topologies induced by the two absolute
values are the same, so
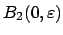
can be covered by
open balls
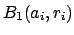
. One of these open balls
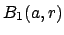
contains
0. There is
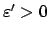
such that
Since
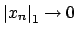
, there exists
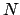
such
that for
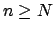
we have
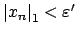
.
For such
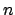
, we have
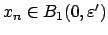
, so
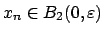
,
so
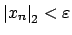
. Thus
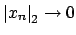
.

Proof.
If
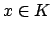
and
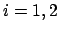
, then
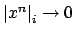
if and only if
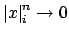
, which is the
case if and only if
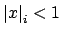
. Thus
Lemma
16.1.3 implies that
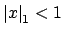
if and only if
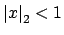
.
On taking reciprocals we see that
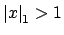
if and only if
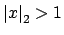
, so finally
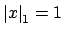
if and only if
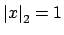
.
Let now 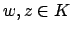 be nonzero elements with
be nonzero elements with
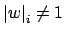 and
and
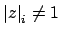 . On
applying the foregoing to
. On
applying the foregoing to
we see that
if and only if
Dividing through by
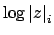
, and rearranging,
we see that for every rational number
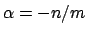
,
Thus
so
Since this equality does not depend on the choice of
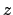
,
we see that there is a constant
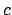
(
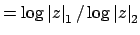
)
such that
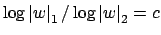
for all
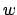
.
Thus
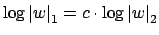
, so
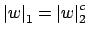
, which implies that
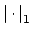
is equivalent to
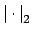
.

![]() to
to ![]() to be
to be
![]() .
Assume for the rest of this section that we only consider valuations
that satisfy the triangle inequality.
.
Assume for the rest of this section that we only consider valuations
that satisfy the triangle inequality.
![]() be nonzero elements with
be nonzero elements with
![]() and
and
![]() . On
applying the foregoing to
. On
applying the foregoing to