Recall (Corollary 5.2.5) that we proved that the
ring of integers  of a number field is Noetherian. As we saw
before using norms, the ring
of a number field is Noetherian. As we saw
before using norms, the ring  is finitely generated as a module
over
is finitely generated as a module
over
 , so it is certainly finitely generated as a ring over
, so it is certainly finitely generated as a ring over
 .
By the Hilbert Basis Theorem,
.
By the Hilbert Basis Theorem,  is Noetherian.
is Noetherian.
If 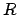 is an integral domain, the of
is an integral domain, the of 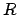 is
the field of all elements
is
the field of all elements 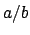 , where
, where 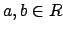 . The field of
fractions of
. The field of
fractions of 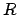 is the smallest field that contains
is the smallest field that contains 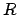 . For
example, the field of fractions of
. For
example, the field of fractions of
 is
is
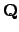 and of
and of
![$ \mathbf{Z}[(1+\sqrt{5})/2]$](img337.png) is
is
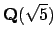 .
.
Definition 6.1.1 (Integrally Closed)
An integral domain
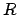
is
if whenever
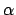
is in the field of fractions of
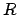
and
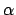
satisfies a monic polynomial
![$ f\in R[x]$](img339.png)
, then
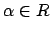
.
Proposition 6.1.2
If 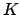 is any number field, then
is any number field, then  is integrally closed. Also,
the ring
is integrally closed. Also,
the ring
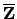 of all algebraic integers is integrally closed.
of all algebraic integers is integrally closed.
Proof.
We first prove that
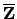
is integrally closed. Suppose
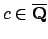
is integral over
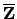
, so there is a monic polynomial
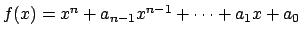
with
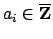
and
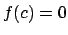
. The
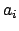
all lie in the ring of integers

of the
number field
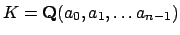
, and

is finitely
generated as a

-module, so
![$ \mathbf{Z}[a_0,\ldots, a_{n-1}]$](img346.png)
is finitely
generated as a

-module. Since
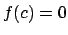
, we can write
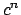
as a
![$ \mathbf{Z}[a_0,\ldots, a_{n-1}]$](img346.png)
-linear combination of
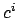
for
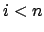
, so
the ring
![$ \mathbf{Z}[a_0,\ldots, a_{n-1},c]$](img350.png)
is also finitely generated as a

-module. Thus
![$ \mathbf{Z}[c]$](img351.png)
is finitely generated as

-module
because it is a submodule of a finitely generated

-module, which
implies that
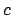
is integral over

.
Suppose 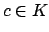 is integral over
is integral over  . Then since
. Then since
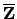 is
integrally closed,
is
integrally closed, 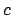 is an element of
is an element of
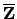 , so
, so
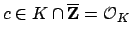 , as required.
, as required.

Definition 6.1.3 (Dedekind Domain)
An integral domain
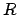
is a
if it is Noetherian,
integrally closed in its field of fractions, and every nonzero prime
ideal of
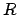
is maximal.
The ring
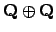 is Noetherian, integrally closed in its field
of fractions, and the two prime ideals are maximal. However, it is
not a Dedekind domain because it is not an integral domain. The ring
is Noetherian, integrally closed in its field
of fractions, and the two prime ideals are maximal. However, it is
not a Dedekind domain because it is not an integral domain. The ring
![$ \mathbf{Z}[\sqrt{5}]$](img356.png) is not a Dedekind domain because it is not integrally
closed in its field of fractions, as
is not a Dedekind domain because it is not integrally
closed in its field of fractions, as
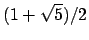 is integrally
over
is integrally
over
 and lies in
and lies in
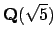 , but not in
, but not in
![$ \mathbf{Z}[\sqrt{5}]$](img356.png) . The
ring
. The
ring
 is a Dedekind domain, as is any ring of integers
is a Dedekind domain, as is any ring of integers  of a
number field, as we will see below. Also, any field
of a
number field, as we will see below. Also, any field 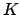 is a Dedekind
domain, since it is a domain, it is trivially integrally closed in
itself, and there are no nonzero prime ideals so that condition that
they be maximal is empty.
is a Dedekind
domain, since it is a domain, it is trivially integrally closed in
itself, and there are no nonzero prime ideals so that condition that
they be maximal is empty.
Proposition 6.1.4
The ring of integers  of a number field is a Dedekind domain.
of a number field is a Dedekind domain.
Proof.
By Proposition
6.1.2, the ring

is
integrally closed, and by Proposition
5.2.5 it is
Noetherian. Suppose that

is a nonzero prime ideal of

.
Let
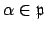
be a nonzero element, and let
![$ f(x)\in\mathbf{Z}[x]$](img359.png)
be the
minimal polynomial of
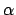
. Then
so
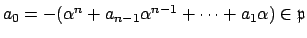
. Since
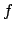
is irreducible,
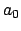
is a nonzero element of

that lies
in

. Every element of the finitely generated abelian group
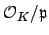
is killed by
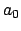
, so
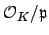
is a finite set.
Since

is prime,
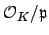
is an integral domain. Every finite
integral domain is a field, so

is maximal, which
completes the proof.

If  and
and 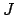 are ideals in a ring
are ideals in a ring 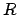 , the product
, the product 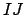 is the ideal
generated by all products of elements in
is the ideal
generated by all products of elements in  with elements in
with elements in 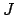 :
:
Note that the set of all products 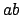 , with
, with 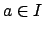 and
and 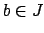 ,
need not be an ideal, so it is important to take the ideal generated
by that set. (See the homework problems for examples.)
,
need not be an ideal, so it is important to take the ideal generated
by that set. (See the homework problems for examples.)
Definition 6.1.5 (Fractional Ideal)
A
is an

-submodule of
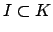
that
is finitely generated as an

-module.
To avoid confusion, we will sometimes call a genuine ideal
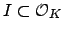 an . Also, since fractional ideals are
finitely generated, we can clear denominators of a generating set to
see that every fractional ideal is of the form
an . Also, since fractional ideals are
finitely generated, we can clear denominators of a generating set to
see that every fractional ideal is of the form
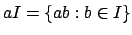 for some
for some 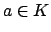 and ideal
and ideal
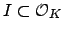 .
.
For example, the collection
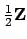 of rational numbers with
denominator
of rational numbers with
denominator 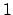 or
or 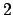 is a fractional ideal of
is a fractional ideal of
 .
.
Theorem 6.1.6
The set of nonzero fractional ideals of a Dedekind domain 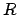 is an
abelian group under ideal multiplication.
is an
abelian group under ideal multiplication.
Before proving Theorem 6.1.6 we prove a lemma. For the
rest of this section  is the ring of integers of a number
field
is the ring of integers of a number
field 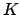 .
.
Definition 6.1.7 (Divides for Ideals)
Suppose that
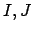
are ideals of

.
Then

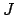
if
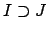
.
To see that this notion of divides is sensible, suppose
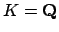 , so
, so
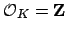 . Then
. Then 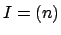 and
and 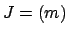 for some integer
for some integer 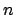 and
and 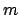 , and
, and
 divides
divides 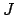 means that
means that
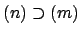 , i.e., that there exists
an integer
, i.e., that there exists
an integer 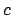 such that
such that  , which exactly means that
, which exactly means that 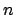 divides
divides
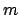 , as expected.
, as expected.
Lemma 6.1.8
Suppose  is an ideal of
is an ideal of  . Then there exist prime ideals
. Then there exist prime ideals
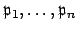 such that
such that
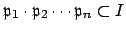 .
In other words,
.
In other words,  divides a product of prime ideals. (By convention
the empty product is the unit ideal. Also, if
divides a product of prime ideals. (By convention
the empty product is the unit ideal. Also, if 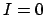 , then we take
, then we take
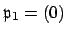 , which is a prime ideal.)
, which is a prime ideal.)
Proof.
The key idea is to use that

is Noetherian to deduce that the
set
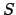
of ideals that do not satisfy the lemma is empty. If
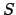
is
nonempty, then because

is Noetherian, there is an ideal
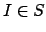
that is maximal as an element of
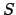
. If

were prime, then

would trivially contain a product of primes, so

is not prime. By
definition of prime ideal, there exists
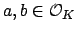
such that
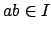
but
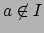
and
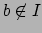
. Let
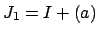
and
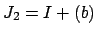
. Then neither
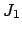
nor
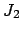
is in
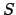
, since

is
maximal, so both
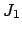
and
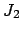
contain a product of prime ideals.
Thus so does

, since
which is a contradiction. Thus
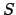
is empty, which completes the proof.

We are now ready to prove the theorem.
Proof.
[Proof of Theorem
6.1.6]
The product of two fractional ideals is again finitely generated, so
it is a fractional ideal, and
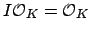
for any nonzero ideal

,
so to prove that the set of fractional ideals under multiplication is
a group it suffices to show the existence of inverses. We will first
prove that if

is a prime ideal, then

has an inverse, then we
will prove that nonzero integral ideals have inverses, and finally
observe that every fractional ideal has an inverse.
Suppose
 is a nonzero prime ideal of
is a nonzero prime ideal of  . We will show that
the
. We will show that
the  -module
-module
is a fractional ideal of

such that
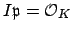
, so that

is an inverse of

.
For the rest of the proof, fix a nonzero element
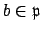 . Since
. Since  is an
is an  -module,
-module,
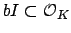 is an
is an  ideal, hence
ideal, hence  is
a fractional ideal. Since
is
a fractional ideal. Since
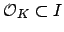 we have
we have
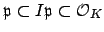 , hence either
, hence either
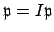 or
or
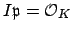 . If
. If
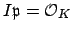 , we are done since then
, we are done since then  is an inverse of
is an inverse of
 . Thus
suppose that
. Thus
suppose that
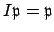 . Our strategy is to show that there is some
. Our strategy is to show that there is some
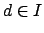 not in
not in  ; such a
; such a 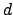 would leave
would leave
 invariant (i.e.,
invariant (i.e.,
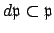 ), so since
), so since
 is an
is an  -module it will follow
that
-module it will follow
that
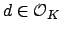 , a contradiction.
, a contradiction.
By Lemma 6.1.8, we can choose a product
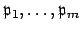 ,
with
,
with 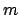 minimal, such that
minimal, such that
If no
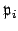
is contained in

, then we can choose for each
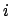
an
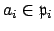
with
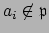
; but then
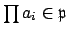
,
which contradicts that

is a prime ideal. Thus some
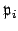
, say
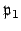
, is contained in

, which implies that
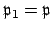
since
every nonzero prime ideal is maximal. Because
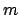
is minimal,
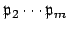
is not a subset of
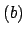
, so there exists
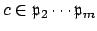
that does not lie in
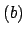
. Then
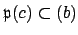
,
so by definition of

we have
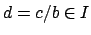
. However,
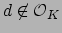
, since if it were then
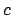
would be in
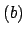
. We have thus
found our element
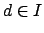
that does not lie in

. To finish the
proof that

has an inverse, we observe that
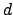
preserves the

-module

, and is hence in

, a contradiction. More
precisely, if
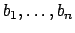
is a basis for

as a

-module,
then the action of
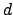
on

is given by a matrix with entries in

, so the minimal polynomial of
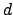
has coefficients in

. This
implies that
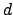
is integral over

, so
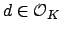
, since

is integrally closed by Proposition
6.1.2.
(Note how this argument depends strongly on the fact that

is
integrally closed!)
So far we have proved that if
 is a prime ideal of
is a prime ideal of  , then
, then
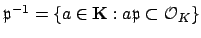 is the inverse of
is the inverse of
 in
the monoid of nonzero fractional ideals of
in
the monoid of nonzero fractional ideals of  . As mentioned after
Definition 6.1.5 [on Tuesday], every nonzero fractional
ideal is of the form
. As mentioned after
Definition 6.1.5 [on Tuesday], every nonzero fractional
ideal is of the form 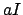 for
for 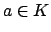 and
and  an integral ideal, so
since
an integral ideal, so
since 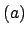 has inverse
has inverse 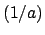 , it suffices to show that every
integral ideal
, it suffices to show that every
integral ideal  has an inverse. If not, then there is a nonzero
integral ideal
has an inverse. If not, then there is a nonzero
integral ideal  that is maximal among all nonzero integral ideals
that do not have an inverse. Every ideal is contained in a maximal
ideal, so there is a nonzero prime ideal
that is maximal among all nonzero integral ideals
that do not have an inverse. Every ideal is contained in a maximal
ideal, so there is a nonzero prime ideal
 such that
such that
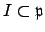 .
Multiplying both sides of this inclusion by
.
Multiplying both sides of this inclusion by
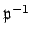 and using that
and using that
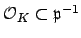 , we see that
, we see that
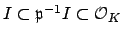 .
If
.
If
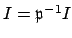 , then arguing as in the proof that
, then arguing as in the proof that
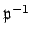 is the
inverse of
is the
inverse of
 , we see that each element of
, we see that each element of
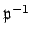 preserves the
finitely generated
preserves the
finitely generated
 -module
-module  and is hence integral. But then
and is hence integral. But then
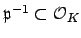 , which implies that
, which implies that
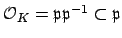 , a contradiction. Thus
, a contradiction. Thus
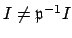 . Because
. Because  is
maximal among ideals that do not have an inverse, the ideal
is
maximal among ideals that do not have an inverse, the ideal
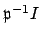 does have an inverse, call it
does have an inverse, call it 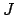 . Then
. Then
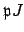 is the inverse of
is the inverse of
 , since
, since
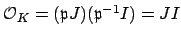 .
.

We can finally deduce the crucial Theorem 6.1.10, which
will allow us to show that any nonzero ideal of a Dedekind domain can
be expressed uniquely as a product of primes (up to order). Thus
unique factorization holds for ideals in a Dedekind domain, and it is
this unique factorization that initially motivated the introduction of
rings of integers of number fields over a century ago.
Proof.
We have
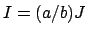
for some
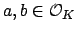
and integral ideal
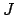
.
Applying Theorem
6.1.10 to
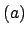
,
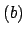
, and
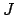
gives
an expression as claimed. For uniqueness, if one has two such product
expressions, multiply through by the denominators and use the
uniqueness part of Theorem
6.1.10

Example 6.1.11
The ring of integers of
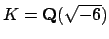
is
![$ \O _K=\mathbf{Z}[\sqrt{-6}]$](img451.png)
.
In

, we have
If
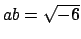
, with
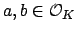
and neither a unit, then

, so without loss
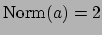
and
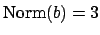
. If
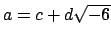
, then
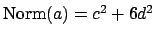
;
since the equation
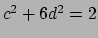
has no solution with
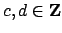
,
there is no element in

with norm
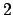
, so
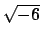
is
irreducible. Also,
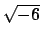
is not a unit times
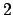
or times
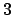
,
since again the norms would not match up. Thus
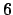
can not be written
uniquely as a product of irreducibles in

.
Theorem
6.1.9, however, implies that the principal
ideal
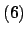
can, however, be
written uniquely as a product of prime ideals. Using
we find such a decomposition:
> R<x> := PolynomialRing(RationalField());
> K := NumberField(x^2+6);
> OK := MaximalOrder(K);
> [K!b : b in Basis(OK)];
[
1,
K.1 // this is sqrt(-6)
]
> Factorization(6*OK);
[
<Prime Ideal of OK
Two element generators:
[2, 0]
[2, 1], 2>,
<Prime Ideal of OK
Two element generators:
[3, 0]
[3, 1], 2>
]
The output means that
where each of the ideals
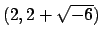
and
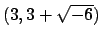
is prime. I will discuss algorithms for computing such a
decomposition in detail, probably next week. The first idea is to
write
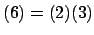
, and hence reduce to the case of writing the
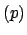
,
for
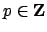
prime, as a product of primes. Next one decomposes the
Artinian ring
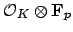
as a product of local Artinian rings.
William Stein
2004-05-06
![]() is an integral domain, the of
is an integral domain, the of ![]() is
the field of all elements
is
the field of all elements ![]() , where
, where ![]() . The field of
fractions of
. The field of
fractions of ![]() is the smallest field that contains
is the smallest field that contains ![]() . For
example, the field of fractions of
. For
example, the field of fractions of
![]() is
is
![]() and of
and of
![]() is
is
![]() .
.
![]() is integral over
is integral over ![]() . Then since
. Then since
![]() is
integrally closed,
is
integrally closed, ![]() is an element of
is an element of
![]() , so
, so
![]() , as required.
, as required.
![]()
![]() and
and ![]() are ideals in a ring
are ideals in a ring ![]() , the product
, the product ![]() is the ideal
generated by all products of elements in
is the ideal
generated by all products of elements in ![]() with elements in
with elements in ![]() :
:
![]() of rational numbers with
denominator
of rational numbers with
denominator ![]() or
or ![]() is a fractional ideal of
is a fractional ideal of
![]() .
.
![]() is a nonzero prime ideal of
is a nonzero prime ideal of ![]() . We will show that
the
. We will show that
the ![]() -module
-module
![]() . Since
. Since ![]() is an
is an ![]() -module,
-module,
![]() is an
is an ![]() ideal, hence
ideal, hence ![]() is
a fractional ideal. Since
is
a fractional ideal. Since
![]() we have
we have
![]() , hence either
, hence either
![]() or
or
![]() . If
. If
![]() , we are done since then
, we are done since then ![]() is an inverse of
is an inverse of
![]() . Thus
suppose that
. Thus
suppose that
![]() . Our strategy is to show that there is some
. Our strategy is to show that there is some
![]() not in
not in ![]() ; such a
; such a ![]() would leave
would leave
![]() invariant (i.e.,
invariant (i.e.,
![]() ), so since
), so since
![]() is an
is an ![]() -module it will follow
that
-module it will follow
that
![]() , a contradiction.
, a contradiction.
![]() ,
with
,
with ![]() minimal, such that
minimal, such that
![]() is a prime ideal of
is a prime ideal of ![]() , then
, then
![]() is the inverse of
is the inverse of
![]() in
the monoid of nonzero fractional ideals of
in
the monoid of nonzero fractional ideals of ![]() . As mentioned after
Definition 6.1.5 [on Tuesday], every nonzero fractional
ideal is of the form
. As mentioned after
Definition 6.1.5 [on Tuesday], every nonzero fractional
ideal is of the form ![]() for
for ![]() and
and ![]() an integral ideal, so
since
an integral ideal, so
since ![]() has inverse
has inverse ![]() , it suffices to show that every
integral ideal
, it suffices to show that every
integral ideal ![]() has an inverse. If not, then there is a nonzero
integral ideal
has an inverse. If not, then there is a nonzero
integral ideal ![]() that is maximal among all nonzero integral ideals
that do not have an inverse. Every ideal is contained in a maximal
ideal, so there is a nonzero prime ideal
that is maximal among all nonzero integral ideals
that do not have an inverse. Every ideal is contained in a maximal
ideal, so there is a nonzero prime ideal
![]() such that
such that
![]() .
Multiplying both sides of this inclusion by
.
Multiplying both sides of this inclusion by
![]() and using that
and using that
![]() , we see that
, we see that
![]() .
If
.
If
![]() , then arguing as in the proof that
, then arguing as in the proof that
![]() is the
inverse of
is the
inverse of
![]() , we see that each element of
, we see that each element of
![]() preserves the
finitely generated
preserves the
finitely generated
![]() -module
-module ![]() and is hence integral. But then
and is hence integral. But then
![]() , which implies that
, which implies that
![]() , a contradiction. Thus
, a contradiction. Thus
![]() . Because
. Because ![]() is
maximal among ideals that do not have an inverse, the ideal
is
maximal among ideals that do not have an inverse, the ideal
![]() does have an inverse, call it
does have an inverse, call it ![]() . Then
. Then
![]() is the inverse of
is the inverse of
![]() , since
, since
![]() .
.
![]()
![]() . If no
. If no
![]() is contained in
is contained in
![]() , then for each
, then for each ![]() there is an
there is an
![]() such that
such that
![]() . But the product of the
. But the product of the ![]() is in the
is in the
![]() , which is a subset of
, which is a subset of
![]() , which contradicts the fact that
, which contradicts the fact that
![]() is a prime ideal. Thus
is a prime ideal. Thus
![]() for some
for some ![]() . We can thus
cancel
. We can thus
cancel
![]() and
and
![]() from both sides of the equation. Repeating
this argument finishes the proof of uniqueness.
from both sides of the equation. Repeating
this argument finishes the proof of uniqueness.
![]()