Unique Factorization of Ideals

In this chapter we will deduce, with complete proofs, the most important basic property of the ring of integers 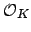$\O _K$ of an algebraic number, namely that every nonzero ideals can be written uniquely as products of prime ideals. After proving this fundamental theorem, we will compute some examples using . The next chapter will consist mostly of examples illustrating the substantial theory we will have already developed, so hang in there!