Summary of Results and The Goal
Theorem 1 (Stein and Grigorov, Jorza, Patrikis, Tarnita)
|
Theorem 1:
Suppose that |
- The proof involves combining refinements of the theorems of Kolyvagin and Kato with
explicit 2 and 3-descents.
- Much work goes into just making this computation
practical.
- One can completely carry it out using SAGE, except for the 3-descents,
which rely on code that Michael Stoll wrote for MAGMA, and three 4-Selmer
group computations, which are also available nowhere but in MAGMA. These
are the only curves in Cremona's book that conjecturally have nontrivial Sha:
571a 681b 960d 960n 4 9 4 4
Theorem 2 (Stein and Lum)
|
Theorem 2:
Suppose that |
- The proof in the rank 0 case is basically an application of a theorem of Rubin.
- When
E has rank 1, a theorem of Mazur and Swinnerton-Dyer givesBSD(E;p) at split primes, and for inert primes we do an explicit Heegner point calculation and use Kolyvagin's bound.
Anticipated Theorem 3 (Stein and Wuthrich)
|
Anticipaed Theorem 3:
Suppose that |
- Wuthrich implemented a program that should
do this in Magma, and I am close to finishing one
that does it in SAGE.
- My goal is that the entire calculation can be completely done
in SAGE (bounding the ranks of three
4 -Selmer groups seems worrisome...)
Once we finish the proof of Theorem 3, we will almost have:
|
Eventual Goal:
Suppose that |
In theory, all that remains is to deal with pairs
-
E is a CM elliptic curve of rank1 with conductor divisible byp , or -
E is a non-CM curve with additive reduction atp such that either-
p divides a Tamagawa number ofE , or - the representation
�E;p is reducible.
-
What is Left?
We finish the talk by computing all pairs
2463 2463 |
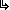
44 44 |
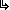
19 19 |
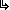
10
[
('121b1', 11),
('225a1', 5),
('361a1', 19),
('441b1', 7),
('441d1', 7),
('675a1', 5),
('784h1', 7),
('800h1', 5),
('800a1', 5),
('900c1', 5)
]
10
[
('121b1', 11),
('225a1', 5),
('361a1', 19),
('441b1', 7),
('441d1', 7),
('675a1', 5),
('784h1', 7),
('800h1', 5),
('800a1', 5),
('900c1', 5)
]
|
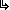
('50a1', 5)
('50b1', 5, 'tamagawa')
('75a1', 5)
('75c1', 5, 'tamagawa')
('121a1', 11)
('121c1', 11)
('150a1', 5)
('150b1', 5)
('175a1', 5)
('175c1', 5)
('225e1', 5)
('225d1', 5)
('275b1', 5)
('294a1', 7)
('294b1', 7)
('325e1', 5, 'tamagawa')
('325d1', 5)
('400b1', 5)
('400c1', 5)
('450a1', 5)
('450b1', 5)
('450c1', 5)
('450d1', 5)
('490f1', 7)
('490k1', 7)
('550f1', 5)
('550k1', 5)
('550b1', 5)
('637a1', 7)
('637c1', 7)
('700d1', 5, 'tamagawa')
('735f1', 7, 'tamagawa')
('775c1', 5)
('882c1', 7)
('882d1', 7)
('950a1', 5)
('975j1', 5, 'tamagawa')
37
('50a1', 5)
('50b1', 5, 'tamagawa')
('75a1', 5)
('75c1', 5, 'tamagawa')
('121a1', 11)
('121c1', 11)
('150a1', 5)
('150b1', 5)
('175a1', 5)
('175c1', 5)
('225e1', 5)
('225d1', 5)
('275b1', 5)
('294a1', 7)
('294b1', 7)
('325e1', 5, 'tamagawa')
('325d1', 5)
('400b1', 5)
('400c1', 5)
('450a1', 5)
('450b1', 5)
('450c1', 5)
('450d1', 5)
('490f1', 7)
('490k1', 7)
('550f1', 5)
('550k1', 5)
('550b1', 5)
('637a1', 7)
('637c1', 7)
('700d1', 5, 'tamagawa')
('735f1', 7, 'tamagawa')
('775c1', 5)
('882c1', 7)
('882d1', 7)
('950a1', 5)
('975j1', 5, 'tamagawa')
37
|