From SAGE 1.0 to SAGE 2.0
One year of hard work by over 30 people...
Leveraging the Internet
The SAGE Notebook
2 + 323
325 325 |
Math typesetting (via jsmath)
jsmath(r'\int_{0}^{2\pi} \frac{\sin(x^2)}{\cos(\theta x)} dx')
|
show(maxima('sin(x^2)').integrate(x))
|
Moin Moin Wiki included standard with SAGE
Trivial to setup wiki pre-configured with math typesetting standard.wiki()
Serving on localhost:9000 localhost - - [19/Jan/2007 16:13:19] "GET / HTTP/1.1" 404 - localhost - - [19/Jan/2007 16:13:20] "GET /MyStartingPage?action=edit HTTP/1.1" 200 - localhost - - [19/Jan/2007 16:13:38] "POST /MyStartingPage HTTP/1.1" 200 - Serving on localhost:9000 localhost - - [19/Jan/2007 16:13:19] "GET / HTTP/1.1" 404 - localhost - - [19/Jan/2007 16:13:20] "GET /MyStartingPage?action=edit HTTP/1.1" 200 - localhost - - [19/Jan/2007 16:13:38] "POST /MyStartingPage HTTP/1.1" 200 - |
Twisted
http://twistedmatrix.com/trac/import twisted help(twisted)
Help on package twisted:
NAME
twisted - Twisted: The Framework Of Your Internet.
FILE
/Users/was/s/local/lib/python2.5/site-packages/twisted/__init__.py
PACKAGE CONTENTS
_version
application (package)
conch (package)
copyright
cred (package)
enterprise (package)
im
internet (package)
lore (package)
mail (package)
manhole (package)
names (package)
news (package)
persisted (package)
plugin
plugins (package)
protocols (package)
python (package)
runner (package)
scripts (package)
spread (package)
tap (package)
test (package)
trial (package)
web (package)
web2 (package)
words (package)
DATA
__version__ = '2.5.0'
version = Version('twisted', 2, 5, 0)
VERSION
2.5.0
Help on package twisted:
NAME
twisted - Twisted: The Framework Of Your Internet.
FILE
/Users/was/s/local/lib/python2.5/site-packages/twisted/__init__.py
PACKAGE CONTENTS
_version
application (package)
conch (package)
copyright
cred (package)
enterprise (package)
im
internet (package)
lore (package)
mail (package)
manhole (package)
names (package)
news (package)
persisted (package)
plugin
plugins (package)
protocols (package)
python (package)
runner (package)
scripts (package)
spread (package)
tap (package)
test (package)
trial (package)
web (package)
web2 (package)
words (package)
DATA
__version__ = '2.5.0'
version = Version('twisted', 2, 5, 0)
VERSION
2.5.0
|
OpenSSL
The inclusion of OpenSSL will be the basis for security for the SAGE notebook and other SAGE related networking work. Also, it will be very useful for security education and research.import OpenSSL help(OpenSSL)
Help on package OpenSSL:
NAME
OpenSSL - pyOpenSSL - A simple wrapper around the OpenSSL library
FILE
/Users/was/s/local/lib/python2.5/site-packages/OpenSSL/__init__.py
PACKAGE CONTENTS
SSL
crypto
rand
tsafe
version
DATA
__version__ = '0.6'
VERSION
0.6
Help on package OpenSSL:
NAME
OpenSSL - pyOpenSSL - A simple wrapper around the OpenSSL library
FILE
/Users/was/s/local/lib/python2.5/site-packages/OpenSSL/__init__.py
PACKAGE CONTENTS
SSL
crypto
rand
tsafe
version
DATA
__version__ = '0.6'
VERSION
0.6
|
Combinatorics and Geometry
gfan -- Tropical Geometry
R.<x,y,z> = QQ[] I = ideal(y^2*z - x^3 - x*z^2) show(I.groebner_fan().reduced_groebner_bases())
|
Polymake
sage: P = polymake.convex_hull([[1,0,0,0], [1,0,0,1], [1,0,1,0], [1,0,1,1], [1,1,0,0], [1,1,0,1], [1,1,1,0], [1,1,1,1]]) # optional: needs polymake sage: P.vertices()
[(1, 0, 0, 0), (1, 0, 0, 1), (1, 0, 1, 0), (1, 0, 1, 1), (1, 1, 0, 0), (1, 1, 0, 1), (1, 1, 1, 0), (1, 1, 1, 1)] [(1, 0, 0, 0), (1, 0, 0, 1), (1, 0, 1, 0), (1, 0, 1, 1), (1, 1, 0, 0), (1, 1, 0, 1), (1, 1, 1, 0), (1, 1, 1, 1)] |
Lattice Polytopes
L = LatticePolytope(matrix(P.vertices())) L.npoints()
Exception (click to the left for traceback): ... Output: Traceback (most recent call last): File " |
L.is_reflexive()
False False |
k = graphs.CubeGraph(5) print k show(k)
5-Cube 5-Cube 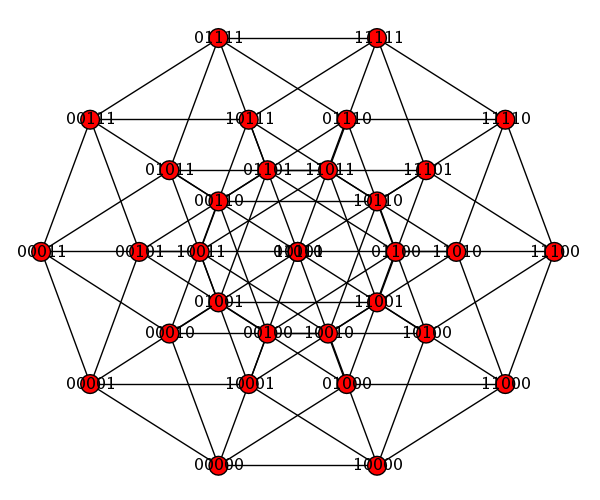
|
Graph Theory -- NetworkX
Number Theory
Many more basic functions
sloane.A000110(23)
44152005855084346 44152005855084346 |
FLINT
print "Coming soon... Will multiply polynomials very quickly."
Coming soon... Will multiply polynomials very quickly. Coming soon... Will multiply polynomials very quickly. |
PARI
A stable 2.3.0 release.gp.version()
((2, 3, 1), 'GP/PARI CALCULATOR Version 2.3.1 (released)') ((2, 3, 1), 'GP/PARI CALCULATOR Version 2.3.1 (released)') |
gp.
Linear Algebra
SageX'ification
This was incredibly difficult! Required substantial improvements to Pyrex, design work, etc.m = matrix(QQ,10,range(100)) type(m)
<type 'sage.matrix.matrix_rational_dense.Matrix_rational_dense'> <type 'sage.matrix.matrix_rational_dense.Matrix_rational_dense'> |
Asymptotically Fast Algorithms
David Harvey, Robert Bradshaw, me -- lots of work to write down general practical algorithms; not just proofs of concept.m.integer_kernel()
Free module of degree 10 and rank 8 over Integer Ring Echelon basis matrix: [ 1 0 0 0 0 0 0 0 -9 8] [ 0 1 0 0 0 0 0 0 -8 7] [ 0 0 1 0 0 0 0 0 -7 6] [ 0 0 0 1 0 0 0 0 -6 5] [ 0 0 0 0 1 0 0 0 -5 4] [ 0 0 0 0 0 1 0 0 -4 3] [ 0 0 0 0 0 0 1 0 -3 2] [ 0 0 0 0 0 0 0 1 -2 1] Free module of degree 10 and rank 8 over Integer Ring Echelon basis matrix: [ 1 0 0 0 0 0 0 0 -9 8] [ 0 1 0 0 0 0 0 0 -8 7] [ 0 0 1 0 0 0 0 0 -7 6] [ 0 0 0 1 0 0 0 0 -6 5] [ 0 0 0 0 1 0 0 0 -5 4] [ 0 0 0 0 0 1 0 0 -4 3] [ 0 0 0 0 0 0 1 0 -3 2] [ 0 0 0 0 0 0 0 1 -2 1] |
Numerical Linear Algebra -- several new choices
Numpy -- work of Travis Oliphantimport numpy numpy.random.
n=1000 m = matrix(RDF,n,range(n^2)) print type(m) time n = m*m
<type 'sage.matrix.matrix_real_double_dense.Matrix_real_double_dense'> Time: CPU 4.89 s, Wall: 5.40 s <type 'sage.matrix.matrix_real_double_dense.Matrix_real_double_dense'> Time: CPU 4.89 s, Wall: 5.40 s |
Developer Tools
Arithmetic Architecture
- Came out of SAGE Days 2
- Has huge impact on speed of SAGE.
- Make using SAGE, adding classes, and understanding implicit coercion much clearer.
- Was incredibly hard to implement, but is now done.
a = 3; b = Mod(8,13) parent(a * b), parent(b*a)
(Ring of integers modulo 13, Ring of integers modulo 13) (Ring of integers modulo 13, Ring of integers modulo 13) |
a._mul_
Pyrex --> SageX
%sagex v = [i*i for i from 0 <= i < 1000] v[2] += 5 print v[:10]
[0, 1, 9, 9, 16, 25, 36, 49, 64, 81] [0, 1, 9, 9, 16, 25, 36, 49, 64, 81]__Users_was_talks_2007_01_19_sage_2_0_sage_notebook_worksheets__scratch__code_sage51_spyx.c |
Darcs --> Mercurial
- Darcs does not scale well; gets slow. Darcs is cool.
- Mercurial scales very well; is fast. Is much much different than Darcs.
hg_sage.
Trac -- bug and feature tracker
http://sage.math.washington.edu:9002/sage_tracGraphics
2d Mathematica-like graphics
def f(x):
return x + sin(x)*cos(x)
show(plot(f, -3, 2, hue=0.7))
def f(x,y):
return cos(x^2 + y^2)
show(contour_plot(f, (-4, 4), (-4, 4), contours=50, cmap="Spectral"))
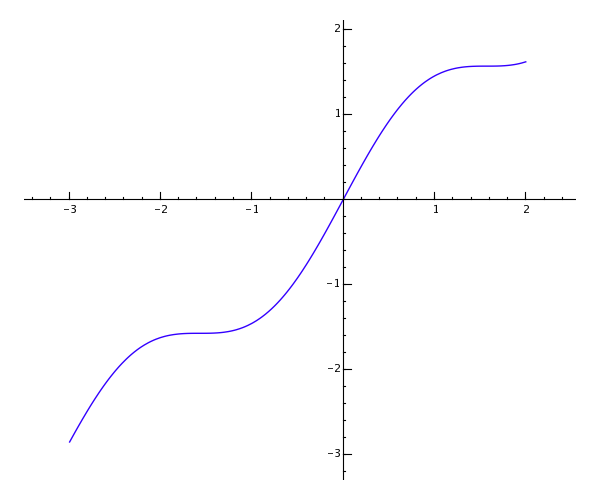 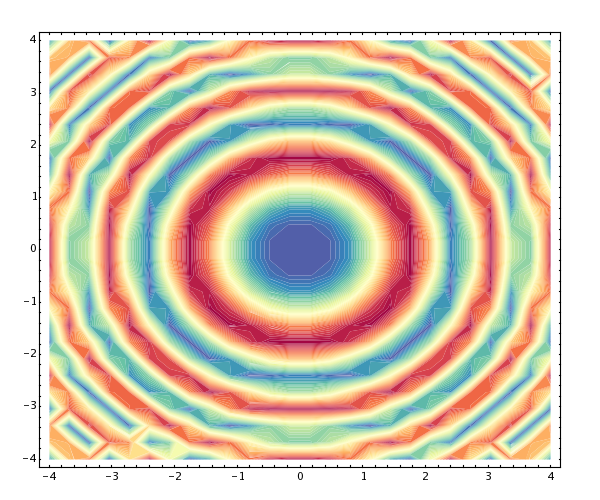
|
3d Raytracer included
sage: t = Tachyon(xres=512,yres=512, camera_center=(2,0.5,0.5), look_at=(0.5,0.5,0.5), raydepth=4)
sage: t.light((4,3,2), 0.2, (1,1,1))
sage: t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,0,0))
sage: t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.3, opacity=1.0, color=(0,1.0,0))
sage: t.texture('t2', ambient=0.2, diffuse=0.7, specular=0.5, opacity=0.7, color=(0,0,1.0))
sage: k=0
sage: for i in range(100):
... k += 1
... t.sphere((random(),random(), random()), random()/10, 't%s'%(k%3))
...
sage: t.save('sage.png')

|
Cryptography
Hart's Optimized Portable Quadratic Sieve
time qsieve(next_prime(10^22)*next_prime(10^25))
([10000000000000000000009, 10000000000000000000000013], '') CPU time: 0.02 s, Wall time: 0.81 s ([10000000000000000000009, 10000000000000000000000013], '') CPU time: 0.02 s, Wall time: 0.81 s |
OpenSSL
import OpenSSL help(OpenSSL)
Help on package OpenSSL:
NAME
OpenSSL - pyOpenSSL - A simple wrapper around the OpenSSL library
FILE
/Users/was/s/local/lib/python2.5/site-packages/OpenSSL/__init__.py
PACKAGE CONTENTS
SSL
crypto
rand
tsafe
version
DATA
__version__ = '0.6'
VERSION
0.6
Help on package OpenSSL:
NAME
OpenSSL - pyOpenSSL - A simple wrapper around the OpenSSL library
FILE
/Users/was/s/local/lib/python2.5/site-packages/OpenSSL/__init__.py
PACKAGE CONTENTS
SSL
crypto
rand
tsafe
version
DATA
__version__ = '0.6'
VERSION
0.6
|
David Kohel's Crypto Package
sage: S = AlphabeticStrings()
sage: E = SubstitutionCryptosystem(S)
sage: E
Substitution cryptosystem on Free alphabetic string monoid on A-Z
sage: K = S([ 25-i for i in range(26) ])
sage: K
ZYXWVUTSRQPONMLKJIHGFEDCBA
sage: e = E(K)
sage: m = S("THECATINTHEHAT")
sage: e(m)
GSVXZGRMGSVSZG
GSVXZGRMGSVSZG GSVXZGRMGSVSZG |
GMP-ECM: Elliptic Curve Factorization Package
time ecm.factor(602400691612422154516282778947806249229526581)
[45949729863572179, 13109994191499930367061460439]
CPU time: 0.01 s, Wall time: 1.64 s
[45949729863572179, 13109994191499930367061460439]
CPU time: 0.01 s, Wall time: 1.64 s
>
> f(p) = p^p -1
>
> where p >= 47 is a prime number.
>
> (for some p's > 47;, gp gave quickly the factorization
> but e.g . for p=47, or p=61, or ?
> gp sems to stay there forever !)
This code in SAGE (version 1.6) splits the p=47 case in about 10-15 minutes:
n=ZZ( (47^47-1)/(2*23*1693))
print n
print "----------\n\n"
print qsieve(n,block=True, verbose=True)
OUTPUT:
[255742492896763511474638530188876017, 194707033016099228267068299180244011637]
so f(47) = 2*23*1693*255742492896763511474638530188876017*194707033016099228267068299180244011637
This code does the same calculation in about 10 minutes also:
n=ZZ( (47^47-1)/(2*23*1693))
print n
print "----------\n\n"
print ecm.factor(n)
OUTPUT:
[255742492896763511474638530188876017, 194707033016099228267068299180244011637]
SAGE is freely available here: http://sage.math.washington.edu/sage/
It includes William Hart's new Quadratic Sieve (which is used for the
first calculation above), and GMP-ECM (which was used for the second
calculation).
A new focus on Calculus, Symbolic Computation, etc.
Clear GOAL: Directly take on Maple/Mathematica for educational application.
Currently going to use Maxima on backend, but maybe also use GIAC (?)
from sage.calculus.all import *
f = sin(x)*cos(3*x) + cos(2*x) - sin(x)^2
show(f.trig_expand())
show(f.integral(x))
sin(x)Ácos(x)3À3Ácos(x)Ásin(x)2À2Ásin(x)2+cos(x)2
8À1Ácos(4Áx)+2sin(2Áx)À2xÀ2sin(2Áx)+4cos(2Áx)
sin(x)Ácos(x)3À3Ácos(x)Ásin(x)2À2Ásin(x)2+cos(x)2
8À1Ácos(4Áx)+2sin(2Áx)À2xÀ2sin(2Áx)+4cos(2Áx)
Numerical Computation
We want to take on MATLAB.
GSL
v = vector(CDF,range(2048))
time w=v.fft()
Time: CPU 0.00 s, Wall: 0.00 s
Time: CPU 0.00 s, Wall: 0.00 s
Numpy
Very matlab like and powerful for a lot of work
SciPy
Optional SAGE package -- provides much more MATLAB like functionality.
WHAT WE REALLY NEED for Education
Integrated environment that is complete, easy to install, and "JUST WORKS". Scipy is not that. SAGE can be.
Distributed Computation
This is just getting going...
Yi Qiang's DSAGE
dsage.[tab] ## doesn't exist yet, but will be very easy to use
time ecm.factor(602400691612422154516282778947806249229526581)
[45949729863572179, 13109994191499930367061460439] CPU time: 0.01 s, Wall time: 1.64 s [45949729863572179, 13109994191499930367061460439] CPU time: 0.01 s, Wall time: 1.64 s |
from sage.calculus.all import * f = sin(x)*cos(3*x) + cos(2*x) - sin(x)^2 show(f.trig_expand()) show(f.integral(x))
|
v = vector(CDF,range(2048)) time w=v.fft()
Time: CPU 0.00 s, Wall: 0.00 s Time: CPU 0.00 s, Wall: 0.00 s |
dsage.[tab] ## doesn't exist yet, but will be very easy to use
Plans for lots of more, which will be a major goal for SAGE 3.0
Clear Decisions about Platform Support, etc
Supported Platforms
- Linux on AMD, x86, and Itanium: as a "monolithic build" only
- OS/X on PPC and Intel: as a "monolithic build" only
- Microsoft Windows: via Cygwin
- Solaris: will be attempted in March
Binary Distribution
http://sage.math.washington.edu/SAGEbin/- Currently a precompiled tarball.
- Anybody can easily make a binary of their personal SAGE install
with their optional packages preinstalled by typing
sage -bdist name
- RPMS, DEBS, MSI's, DPKG will come when the time is right, i.e., when we are ready to have way more users than developers; this will be by the end of March.