Bibliography

Aga99b

A.Agashe, On invisible elements of the Tate-Shafarevich group, C. R. Acad. Sci. Paris Sér. I Math. 328 (1999), no. 5, 369-374.

AS02

A.Agashe and W.A. Stein, Visibility of Shafarevich-Tate groups of abelian varieties, J. Number Theory 97 (2002), no. 1, 171-185.

AS05

A. Agashe and W. Stein, Visible evidence for the Birch and Swinnerton-Dyer conjecture for modular abelian varieties of analytic rank zero, Math. Comp. 74 (2005), no. 249, 455-484 (electronic), With an appendix by J. Cremona and B. Mazur.

ARS06

A. Agashe, K.A. Ribet and W. Stein, The Manin constant, to appear in Quarterly J. of Pure and Applied Math. volume in honor of J. Coates.

AM69

M.F. Atiyah and I.G.Macdonald, Introduction to commutative algebra, Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont., (1969).

BCDT01

C. Breuil, B. Conrad, F. Diamond, and R. Taylor, On the modularity of elliptic curves over 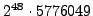$\bold Q$ : wild 3-adic exercises, J. Amer. Math. Soc. 14 (2001), no. 4, 843-939 (electronic).

BCP97

W. Bosma, J. Cannon, and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), no. 3-4, 235-265, Computational algebra and number theory (London, 1993).

CW06

M.Ciperiani, A.Wiles, Solvable points on genus one curves, preprint (2006).

CFK06

C.David, J.Fearnly, H.Kisilevsky, Vanishing of twisted 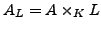$L$ -functions of elliptic curves, to appear in Experiment. Math.

CM00

J.E. Cremona and B. Mazur, Visualizing elements in the Shafarevich-Tate group, Experiment. Math. 9 (2000), no. 1, 13-28.

CV92

R.F. Coleman, J.F. Voloch, Companion forms and Kodaira-Spencer theory, Invent. Math., 110, (1992), 2, 263-281.

CS01

B.Conrad, W.A. Stein, Component groups of purely toric quotients, Math. Res. Lett., 8, 5-6, (2001), 745-766.

Cre

J.E. Cremona, Tables of Elliptic Curves,
http://www.maths.nott.ac.uk/personal/jec/ftp/data/

CR62

C.W. Curtis and I. Reiner, Representation theory of finite groups and associative algebras, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1962, Pure and Applied Mathematics, Vol. XI.

Fal86

G. Faltings, Finiteness theorems for abelian varieties over number fields, Arithmetic geometry (Storrs, Conn., 1984), Springer, New York, 1986, Translated from the German original [Invent. Math. 73 (1983), no. 3, 349-366; ibid. 75 (1984), no. 2, 381] by Edward Shipz, pp. 9-27.

Ka81

N.M. Katz, Galois properties of torsion points on abelian varieties, Invent. Math. 62 (1981), no. 3, 481-502.

Kle01

T. Klenke, Modular Varieties and Visibility, Ph.D. thesis, Harvard University (2001).

KS00

D.R. Kohel and W.A. Stein, Component Groups of Quotients of 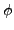$J_0(N)$ , Proc. ANTS-IV, Springer, 2000.

KL89

V.A. Kolyvagin and D.Y. Logachev, Finiteness of the Shafarevich-Tate group and the group of rational points for some modular abelian varieties, Algebra i Analiz 1 (1989), no. 5, 171-196.

Maz77

B.Mazur, Modular curves and the Eisenstein ideal, Inst. Hautes Études Sci. Publ. Math., 47, (1977), 33-186.

Maz99

to3em, Visualizing elements of order three in the Shafarevich-Tate group, Asian J. Math. 3 (1999), no. 1, 221-232, Sir Michael Atiyah: a great mathematician of the twentieth century.

Mil72

J.S. Milne, On the arithmetic of abelian varieties, Invent. Math. 17 (1972), 177-190.

Mil86

to3em, Arithmetic duality theorems, Academic Press Inc., Boston, Mass., (1986), x+421.

Rib83

K.A. Ribet, Congruence relations between modular forms, Proc. International Congress of Mathematicians, 503-514, (1983).

Rib87

to3em, On the component groups and the Shimura subgroup of 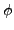$J_0(N)$ , Séminaire de Théorie des Nombres, 1987-1988 (Talence, 1987-1988), Exp. No. 6, 10, Univ. Bordeaux I.

Rib90a

to3em, On modular representations of 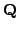${\rm {G}al}(\overline{\bf {Q}}/{\bf {Q}})$ arising from modular forms, Invent. Math., 100 1990, no. 2, 431-476.

Rib90b

to3em, Raising the levels of modular representations, Séminaire de Théorie des Nombres, Paris 1987-88, Birkhäuser Boston, Boston, MA, 1990, pp. 259-271.

Rib91

to3em, Lowering the levels of modular representations without multiplicity one, International Mathematics Research Notices, (1991), 15-19.

Rib92

to3em, Abelian varieties over 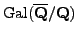${\bf Q}$ and modular forms, Algebra and topology 1992 (Taejon), Korea Adv. Inst. Sci. Tech., Taejon, 1992, pp. 53-79.

RS01

K.A. Ribet and W.A. Stein, Lectures on Serre's conjectures, Arithmetic algebraic geometry (Park City, UT, 1999), IAS/Park City Math. Ser., 9, 143-232, Amer. Math. Soc., Providence, RI, (2001).

Rub89

K.Rubin, The work of Kolyvagin on the arithmetic of elliptic curves, Arithmetic of complex manifolds (Erlangen, 1988), 128-136, Springer, Berlin, (1989).

Se79

J-P.Serre, Local fields, Springer-Verlag, New York, (1979).

Shi94

G.Shimura, Introduction to the arithmetic theory of automorphic functions, reprint of the 1971 original, Kan Memorial Lectures, 1, Princeton University Press, (1994).

Ste00

W.A. Stein, Explicit approaches to modular abelian varieties, Ph.D. thesis, University of California, Berkeley (2000).

Ste04

W.A. Stein, Shafarevich-Tate Groups of Nonsquare Order, Modular Curves and Abelian Varieties, Progress of Mathematics (2004), 277-289.

Stu87

J.Sturm, On the congruence of modular forms, Number theory (New York, 1984-1985), Springer, Berlin (1987), 275-280.

Wil95

A.J. Wiles, Modular elliptic curves and Fermat's last theorem, Ann. of Math. (2), 141(3), (1995), 443-551.

1000