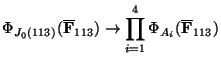Theorem 7.2 (Emerton)
Let
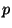
be a prime and let
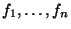
be a set of
representatives for the Galois-conjugacy classes of newforms
in
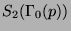
. Let
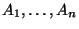
be the optimal
quotients associated to
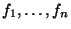
, respectively.
Then for each
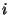
,
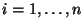
, we have
Furthermore,
Before Emerton proved the above assertion, the second author verified it
using the algorithm of this paper for all 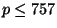 , and, up to a
power of
, and, up to a
power of 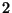 , for all
, for all 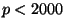 .
.
Remark 7.3
It is tempting to guess that, e.g., the natural map
is an isomorphism, but this is incorrect. Two of the
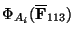
have order
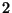
, so the product
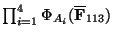
is not a cyclic group.
However, Mazur proved that the groups
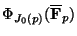
are
cyclic for all primes
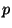
.
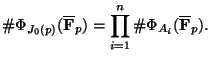
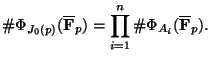
![]() , and, up to a
power of
, and, up to a
power of ![]() , for all
, for all ![]() .
.