A congruence subgroup is a subgroup of the group
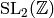 of determinant
of determinant 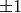 integer
matrices that contains
integer
matrices that contains
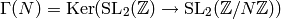
for some positive integer 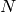 . Since
. Since 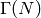 has
finite index in
has
finite index in 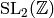 , all congruence subgroups
have finite index. The converse is not true, though in many other
settings it is true (see [paper of Serre]).
, all congruence subgroups
have finite index. The converse is not true, though in many other
settings it is true (see [paper of Serre]).
The inverse image 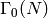 of the subgroup of upper
triangular matrices in
of the subgroup of upper
triangular matrices in 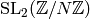 is a congruence subgroup, as is the inverse image
is a congruence subgroup, as is the inverse image 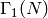 of the subgroup of matrices of the form
of the subgroup of matrices of the form
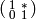 . Also,
for any subgroup
. Also,
for any subgroup  , the
inverse image
, the
inverse image 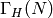 of the subgroup of
of the subgroup of
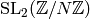 of all elements of the
form
of all elements of the
form 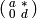 with
with 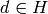 is a congruence subgroup.
is a congruence subgroup.
We can create each of the above congruence subgroups in Sage, using the Gamma0, Gamma1, and GammaH commands.
sage: Gamma0(8)
Congruence Subgroup Gamma0(8)
sage: Gamma1(13)
Congruence Subgroup Gamma1(13)
sage: GammaH(11,[2])
Congruence Subgroup Gamma_H(11) with H generated by [2]
The second argument to the GammaH command is a list of generators of
the subgroup 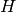 of
of 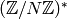 .
.
Sage can compute a list of generators for these subgroups. The algorithm Sage uses is a straightforward generic procedure that uses coset representatives for the congruence subgroup (which are easy to enumerate) to obtain a list of generators [[ref my modular forms book]].
sage: Gamma0(2).gens()
([1 1]
[0 1],
[-1 0]
[ 0 -1],
[ 1 -1]
[ 0 1],
[ 1 -1]
[ 2 -1],
[-1 1]
[-2 1])
sage: len(Gamma1(13).gens())
284
As you can see above, the list of generators Sage computes is unfortunately large. Improving this would be an excellent Sage development project, which would involve much beautiful mathematics.
A modular form on a congruence subgroup
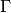 of integer weight
of integer weight 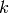 is a holomorphic
function
is a holomorphic
function 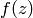 on the upper half plane
on the upper half plane
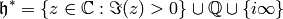
such that for every matrix
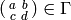 ,
we have
,
we have
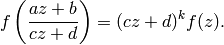
A cusp form is a modular form that vanishes at all of the cusps
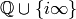 .
.
If 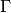 contains
contains 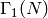 for some
for some 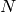 ,
then
,
then
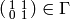 ,
so the modular form condition implies that
,
so the modular form condition implies that 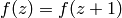 . This, coupled
with the holomorphicity condition, implies that
. This, coupled
with the holomorphicity condition, implies that 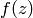 has a
Fourier expansion
has a
Fourier expansion
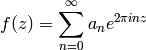
with 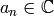 . We let
. We let 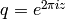 , and
call
, and
call 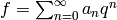 the
the 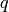 -expansion
of
-expansion
of 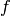 .
.
Henceforth we assume that
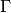 is either
is either 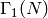 ,
,
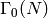 , or
, or 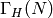 for some
for some
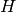 and
and 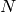 . The complex vector space
. The complex vector space
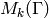 of all modular forms of weight
of all modular forms of weight 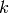 on
on 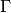 is a finite dimensional vector space.
is a finite dimensional vector space.
We create the space 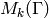 in Sage by typing
ModularForms(G, k) where
in Sage by typing
ModularForms(G, k) where 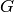 is the congruence subgroup
and
is the congruence subgroup
and 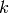 is the weight.
is the weight.
sage: ModularForms(Gamma0(25), 4)
Modular Forms space of dimension 11 for ...
sage: S = CuspForms(Gamma0(25),4, prec=15); S
Cuspidal subspace of dimension 5 of Modular Forms space ...
sage: S.basis()
[
q + q^9 - 8*q^11 - 8*q^14 + O(q^15),
q^2 - q^7 - q^8 - 7*q^12 + 7*q^13 + O(q^15),
q^3 + q^7 - 2*q^8 - 6*q^12 - 5*q^13 + O(q^15),
q^4 - q^6 - 3*q^9 + 5*q^11 - 2*q^14 + O(q^15),
q^5 - 4*q^10 + O(q^15)
]
Sage computes the dimensions of all these spaces using simple arithmetic formulas instead of actually computing bases for the spaces in question. In fact, Sage has the most general collection of modular forms dimension formulas of any software; type help(sage.modular.dims) to see a list of arithmetic functions that are used to implement these dimension formulas.
sage: ModularForms(Gamma1(949284), 456).dimension()
11156973844800
sage: a = [dimension_cusp_forms(Gamma0(N),2) for N in [1..25]]; a
[0, 0, ..., 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 2, 2, 1, 0]
sage: sloane_find(a)
Searching Sloane's online database...
[[1617,
'Genus of modular group GAMMA_0 (n). Or, genus of
modular curve X_0(n).',...
Sage doesn’t have simple formulas for dimensions of spaces of
modular forms of weight 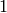 , since such formulas perhaps do
not exist.
, since such formulas perhaps do
not exist.
The space
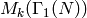 is equipped with an action of
is equipped with an action of
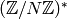 by diamond bracket operators
by diamond bracket operators
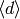 , and this induces a decomposition
, and this induces a decomposition
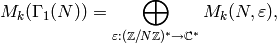
where the sum is over all complex characters of the
finite abelian group 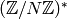 . These
characters are called Dirichlet characters, which are central in
number theory.
. These
characters are called Dirichlet characters, which are central in
number theory.
The factors 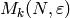 then have bases whose
then have bases whose
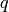 -expansions are elements of
-expansions are elements of ![R[[q]]](_images/math/df866ccab32997ce6003a384eb6859e547310691.png) , where
, where
![R = \mathbb{Z}[\varepsilon]](_images/math/6033beea3420b65d1c31920400915826513baf23.png) is the ring generated over
is the ring generated over
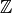 by the image of
by the image of  . We illustrate
this with
. We illustrate
this with  below, where DirichletGroup will be
described later.
below, where DirichletGroup will be
described later.
sage: CuspForms(DirichletGroup(5).0, 5).basis()
[q + (-zeta4 - 1)*q^2 + (6*zeta4 - 6)*q^3 - ... + O(q^6)]
Use the command DirichletGroup(N,R) to create the group of all
Dirichlet characters of modulus 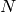 taking values in the
ring
taking values in the
ring 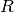 . If
. If 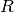 is omited, it defaults to a
cyclotomic field.
is omited, it defaults to a
cyclotomic field.
sage: G = DirichletGroup(8); G
Group of Dirichlet characters of modulus 8 over Cyclotomic
Field of order 2 and degree 1
sage: v = G.list(); v
[[1, 1], [-1, 1], [1, -1], [-1, -1]]
sage: eps = G.0; eps
[-1, 1]
sage: [eps(3), eps(5)]
[-1, 1]
Sage both represents Dirichlet characters by giving a “matrix”,
i.e., the list of images of canonical generators of
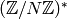 , and as vectors modulo and
integer
, and as vectors modulo and
integer 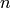 . For years, I was torn between these two
representations, until J. Quer and I realized that the best
approach is to use both and make it easy to convert between them.
. For years, I was torn between these two
representations, until J. Quer and I realized that the best
approach is to use both and make it easy to convert between them.
sage: parent(eps.element())
Vector space of dimension 2 over Ring of integers modulo 2
Given a Dirichlet character, Sage also lets you compute the associated Jacobi and Gauss sums, generalized Bernoulli numbers, the conductor, Galois orbit, etc.
 ¶
¶Recall that Dirichlet characters give a decomposition
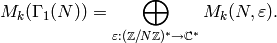
Given a Dirichlet character  we type
ModularForms(eps, weight) to create the space of modular forms with
that character and a given integer weight. For example, we create
the space of forms of weight
we type
ModularForms(eps, weight) to create the space of modular forms with
that character and a given integer weight. For example, we create
the space of forms of weight 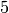 with the character modulo
with the character modulo
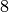 above that is
above that is 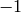 on
on 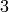 and
and
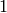 on
on 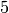 as follows.
as follows.
sage: ModularForms(eps,5)
Modular Forms space of dimension 6, character [-1, 1] and
weight 5 over Rational Field
sage: sum([ModularForms(eps,5).dimension() for eps in v])
11
sage: ModularForms(Gamma1(8),5)
Modular Forms space of dimension 11 ...
Note
Exercise: Compute the dimensions of all spaces 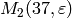 for all Dirichlet characters
for all Dirichlet characters  .
.
The space 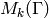 is equipped with an action of a commuting ring
is equipped with an action of a commuting ring 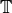 of
Hecke operators
of
Hecke operators 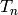 for
for 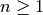 . A standard
computational problem in the theory of modular forms is to compute
an explicit basis of
. A standard
computational problem in the theory of modular forms is to compute
an explicit basis of 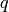 -expansion for
-expansion for
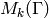 along with matrices for the action of any
Hecke operator
along with matrices for the action of any
Hecke operator 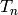 , and to compute the subspace
, and to compute the subspace
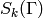 of cusp forms.
of cusp forms.
sage: M = ModularForms(Gamma0(11),4)
sage: M.basis()
[
q + 3*q^3 - 6*q^4 - 7*q^5 + O(q^6),
q^2 - 4*q^3 + 2*q^4 + 8*q^5 + O(q^6),
1 + O(q^6),
q + 9*q^2 + 28*q^3 + 73*q^4 + 126*q^5 + O(q^6)
]
sage: M.hecke_matrix(2)
[0 2 0 0]
[1 2 0 0]
[0 0 9 0]
[0 0 0 9]
We can also compute Hecke operators on the cuspidal subspace.
sage: S = M.cuspidal_subspace()
sage: S.hecke_matrix(2)
[0 2]
[1 2]
sage: S.hecke_matrix(3)
[ 3 -8]
[-4 -5]
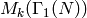 ¶
¶Unfortunately, Sage doesn’t yet implement computation of the Hecke
operators on 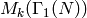 .
.
sage: M = ModularForms(Gamma1(5),2)
sage: M
Modular Forms space of dimension 3 for Congruence Subgroup
Gamma1(5) of weight 2 over Rational Field
sage: M.hecke_matrix(2)
...
NotImplementedError
However, we can compute Hecke operators on modular symbols for
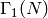 , which is a
, which is a  -module that is
isomorphic to
-module that is
isomorphic to 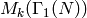 (see
Modular Symbols).
(see
Modular Symbols).
sage: ModularSymbols(Gamma1(5),2,sign=1).hecke_matrix(2)
[ 2 1 1]
[ 1 2 -1]
[ 0 0 -1]