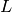 -series¶
-series¶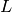 -series of
-series of 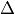 ¶
¶Thanks to wrapping work of Jennifer Balakrishnan of M.I.T., we can
compute explicitly with the 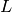 -series of the modular form
-series of the modular form
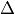 . Like for elliptic curves, behind these scenes
this uses Dokchitsers
. Like for elliptic curves, behind these scenes
this uses Dokchitsers 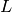 -functions calculation Pari
program.
-functions calculation Pari
program.
sage: L = delta_lseries(); L
L-series associated to the modular form Delta
sage: L(1)
0.0374412812685155
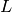 -series of a Cusp Form¶
-series of a Cusp Form¶In some cases we can also compute with
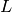 -series attached to a cusp form.
-series attached to a cusp form.
sage: f = CuspForms(2,8).0
sage: L = f.cuspform_lseries()
sage: L(1)
0.0884317737041015
sage: L(0.5)
0.0296568512531983
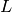 -series of a General Newform is Not Implemented¶
-series of a General Newform is Not Implemented¶Unfortunately, computing with the 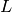 -series of a general newform is not
yet implemented.
-series of a general newform is not
yet implemented.
sage: S = CuspForms(23,2); S
Cuspidal subspace of dimension 2 of Modular Forms space of
dimension 3 for Congruence Subgroup Gamma0(23) of weight
2 over Rational Field
sage: f = S.newforms('a')[0]; f
q + a0*q^2 + (-2*a0 - 1)*q^3 + (-a0 - 1)*q^4 + 2*a0*q^5 + O(q^6)
Computing with 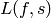 totally not implemented yet, though
should be easy via Dokchitser.
totally not implemented yet, though
should be easy via Dokchitser.