Problem 8.8.2
Cristian Wuthrich and Stein (mostly Wuthrich) have written a bunch
of code related to using Peter Schneider's work on

-adic
analogues of the BSD conjecture to compute
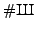
at certain
primes where the methods of Kolyvagin and Kato fail.
Remark 8.8.3 (From Christian Wuthrich.)
Note that the paper mentioned above, as
far as I have written it is, to my taste, more or less done. I
should add some data of numerical results which you can of course
ask the students to produce. But there is no need or interest for a
long list. I have not written yet the introduction nor the part I
named technical details (but I am not sure if I actually want to do
that).
Of course, I am very happy that part (or the whole of) shark will be
included in SAGE.
Remark 8.8.4 (From Christian Wuthrich.)
Schneider's (and simultanoeously
Perrin-Riou's work) is strictly speaking not on the p-adic BSD. The
most important result to use is Kato's which links the algebraic to
the analytic side. Look in the article we write together for a
tigher bound in the case
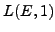
is not zero. Your katobound in
sage is not sharp.