Big images

This section was written by Gabor Wiese.

To every mod 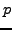$p$ eigenform Deligne attaches a 2-dimensional odd "mod 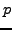$p$ " Galois representation, i.e. a continuous group homomorphism

$${\mathrm{Gal}}(\overline{\mathbb{Q}}/\mathbb{Q}) \to {\mathrm{GL}}_2(\overline{\mathbb{F}}_p).$$

The trace of a Frobenius element at a prime 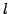$l$ is for almost all 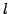$l$ given by the 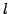$l$ -th coefficient of the (normalised) eigenform. By continuity, the image of such a representation is a finite group.

Problem 2.1.1   Find group theoretic criteria that allow one (in some cases) to determine the image computationally.

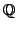
Remark 2.1.2 (From Richard Taylor)   Problem 2.1.1 seems to me straightforward. (Richard, Grigor, and Stein did something like this for elliptic curves over $\mathbb{Q}$ -- see http://modular.math.washington.edu/papers/bsdalg/.)

Problem 2.1.3   Implement in SAGE the algorithm of Problem 2.1.1.

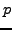
Problem 2.1.4   Carry out systematic computations of mod $p$ modular forms in order to find ``big'' images.

Like this one can certainly realise some groups as Galois groups over 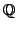$\mathbb{Q}$ that were not known to occur before!