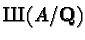using
only congruences between elliptic curves is bound to fail.
This is because pairs of nonisogenous elliptic curves
with isomorphic p-torsion are, according to
E. Kani's conjecture, extremely rare.
It is crucial to understand what happens in all dimensions.
Within the range accessible by computer, abelian varieties exhibit more richly textured structure than elliptic curves. For example, I discovered a visible element of prime order 83341in the Shafarevich-Tate group of an abelian variety of prime conductor 2333; in contrast, over all optimal elliptic curves of conductor up to 5500, it appears that the largest order of an element of a Shafarevich-Tate group is 7.