William Stein's homepage

Genus one curves

The index of an algebraic curve C over  Q is the order of the cokernel of the degree map 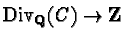$\mbox{\rm Div}_\mathbf{Q}(C)\rightarrow\mathbf{Z}$; rationality of the canonical divisor implies that the index divides 2g-2, where g is the genus of C. When g=1 this is no condition at all; Artin conjectured, and Lang and Tate [14] proved, that for every integer mthere is a genus one curve of index m over some number field. Their construction yields genus one curves over  Q only for a few values of m, and they ask whether one can find genus one curves over  Q of every index. I have answered this question for odd m.

Theorem 8   Let K be any number field. There are genus one curves over K of every odd index.

The proof involves showing that enough cohomology classes in Kolyvagin's Euler system of Heegner points do not vanish combined with explicit Heegner point computations. I hope to show that curves of every index occur, and to determine the consequences of my nonvanishing result for Selmer groups. This can be viewed as a contribution to the problem of understanding H¹(Q,E).