William Stein's homepage



Next: Cyclotomic points on modular
Up: Conjectures of Artin and
Previous: Conjectures of Artin and
E. Artin conjectured in [3]
that the L-series associated to any continuous irreducible
representation
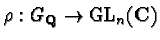 ,
with n>1, is entire.
Recent exciting work of Taylor and others suggests that a complete proof
of Artin's conjecture, in the case when n=2 and
,
with n>1, is entire.
Recent exciting work of Taylor and others suggests that a complete proof
of Artin's conjecture, in the case when n=2 and 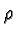 is odd,
is on the horizon.
This case of Artin's conjecture is known when the image
of
is odd,
is on the horizon.
This case of Artin's conjecture is known when the image
of 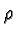 in
in
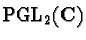 is solvable
(see [27]), and in infinitely
many cases when the image of
is solvable
(see [27]), and in infinitely
many cases when the image of 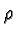 is not solvable (see [7]).
is not solvable (see [7]).
In 1998, K. Buzzard suggested a way to combine the
main theorem of [8], along with
a computer computation, to deduce modularity of certain
icosahedral Galois representations. Buzzard and I recently obtained
the following theorem.
Theorem 6
The icosahedral Artin representations of conductor
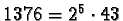
are modular.
We expect our method to yield several more examples.
These ongoing computations are laying a small part of the technical
foundations necessary for a full proof of the Artin conjecture
for odd two dimensional 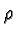 ,
as well as stimulating
the development of new algorithms for computing with modular forms
using modular symbols in characteristic
,
as well as stimulating
the development of new algorithms for computing with modular forms
using modular symbols in characteristic 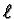 .
.
William A. Stein
1999-12-01