Next: Indefinite Integrals and Change Up: The Definite Integral Previous: Definition of Integral Contents Index
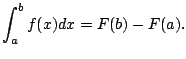
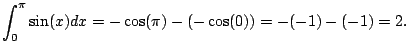
But does such an ![]() always exist? The surprising answer is ``yes''.
always exist? The surprising answer is ``yes''.
Note that a ``nice formula'' for
The proof of Theorem 2.1.5 is somewhat complicated but is given in complete detail in Stewart's book, and you should definitely read and understand it.
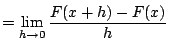 |
||
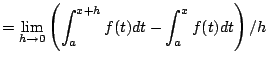 |
||
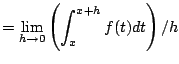 |
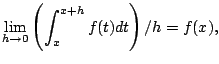
William Stein 2006-03-15