Next: Shift the Origin Up: Sequences and Series Previous: The Root Test Contents Index
| Final exam: Wednesday, March 22, 7-10pm in PCYNH 109. Bring ID!
Quiz 4: This Friday Today: 11.8 Power Series, 11.9 Functions defined by power series Next: 11.10 Taylor and Maclaurin series |
Recall that a polynomial is a function of the form
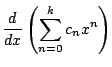 |
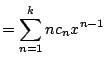 |
|
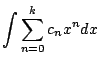 |
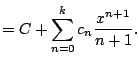 |
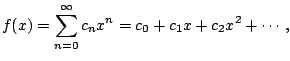
A power series is a function of ![]() for those
for those ![]() for
which it converges.
for
which it converges.
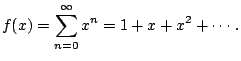
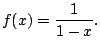
But what good could this possibly be? Why is writing the simple
function
![]() as the complicated series
as the complicated series
![]() of any value?
of any value?
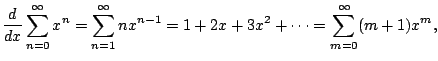
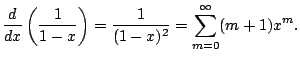
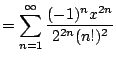 |
||
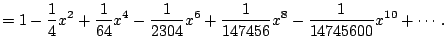 |