Next: The Integral and Comparison Up: Sequences and Series Previous: Sequences Contents Index
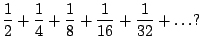
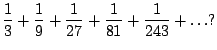
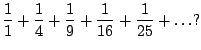
Consider the following sequence of partial sums:
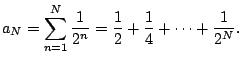
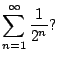
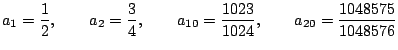
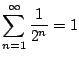 , if it makes
any sense. But does it?
, if it makes
any sense. But does it?
In a moment we will define
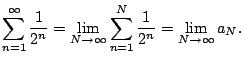
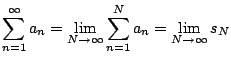
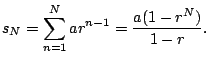
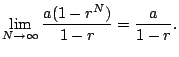
For example, if ![]() and
and
![]() , we get
, we get
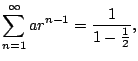
William Stein 2006-03-15