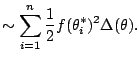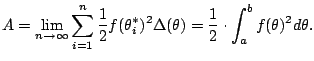Next: Examples Up: Polar Coordinates and Complex Previous: Polar Coordinates Contents Index
| Exam 1 Wed Feb 1 7:00pm in Pepper Canyon 109 (not 106!! different class there!)
Office hours: 2:45pm-4:15pm Next: Complex numbers (appendix G); complex exponentials (supplement, which is freely available online). We will not do arc length.
People were most confused last time by plotting curves in polar
coordinates. (1) it is tedious, but easier if you do a few and
know what they look like (just plot some points and see); there's not
much to it, except plug in values and see what you get, and (2) can
sometimes convert to a curve in GOAL for today: Integration in the context of polar coordinates. Get much better at working with polar coordinates! |
Multiplying both sides of the equation
![]() by
by ![]() yields
yields
But it isn't... if we remember the basic idea of calculus: subdivide and take a limit.
[[Draw a section of a curve
![]() for
for ![]() in some interval
in some interval
![]() , and shade in the area of the arc.]]
, and shade in the area of the arc.]]
We know how to compute the area of a sector, i.e., piece of a circle
with angle ![]() . [[draw picture]]. This is the basic polar region.
The area is
. [[draw picture]]. This is the basic polar region.
The area is
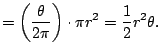
We now imitate what we did before with Riemann sums. We chop
up, approximate, and take a limit.
Break the interval of angles from ![]() to
to ![]() into
into ![]() subintervals.
Choose
subintervals.
Choose
![]() in each interval.
The area of each slice is approximately
in each interval.
The area of each slice is approximately
![]() .
Thus
.
Thus