Homework reminder.
Quiz reminder: Friday, Jan 20
(Ace the first quiz!).
Office Hours: Tue 11-1.
Monday is a holiday!
Wednesday - areas between curves and volumes
First midterm: Wed Feb 1 at 7pm (review lecture during day!)
Quick 5 minute discussion of computers and Maxima.
Quiz format: one question on front; one on back.
Remarks:
- The total distance traveled is
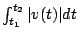 since since
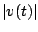 is the rate of change of is the rate of change of 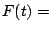 distance traveled (your
speedometer displays the rate of change of your odometer). distance traveled (your
speedometer displays the rate of change of your odometer).
- How to compute
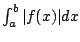 . .
- Find the zeros of
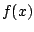 on on ![$ [a,b]$](img17.png) , and use these to break
the interval up into subintervals on which , and use these to break
the interval up into subintervals on which 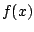 is always is always 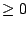 or always
or always 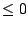 . .
- On the intervals where
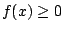 , compute the integral of , compute the integral of 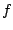 ,
and on the intervals where ,
and on the intervals where
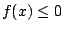 , compute the integral of , compute the integral of 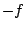 . .
- The sum of the above integrals on intervals is
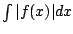 . .
|