Trigonometric Integrals
Friday: Quiz 2
Next: Trig subst.
|
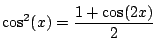 and and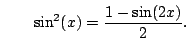 |
(5.2) |
|
Example 5.2.1
Compute
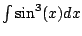
.
We use trig. identities and compute the integral directly as follows:
This always works for odd powers of
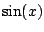
.
Example 5.2.2
What about
even powers?!
Compute
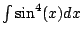
.
We have
Thus
Key Trick: Realize that we should write
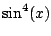
as
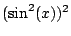
. The rest is straightforward.
Example 5.2.3
This example illustrates a method for computing integrals of trig
functions that doesn't require knowing any trig identities at all or
any tricks. It is very tedious though. We compute
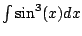
using
complex exponentials. We have
hence
The answer looks totally different, but is in fact the same function.
Here are some more identities that we'll use in illustrating some tricks
below.
Example 5.2.4
Compute
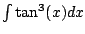
.
We have
Here we used the substitution
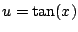
, so
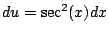
,
so
Also, with the substitution
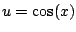
and
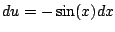
we get
Key trick: Write
 as
as
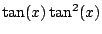 .
.
Example 5.2.5
Here's one that combines trig identities with the funnest
variant of integration by parts.
Compute
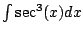 .
.
We have
Let's use integration by parts.
The above integral becomes
This is familiar. Solve for
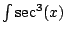
. We get
Subsections
William Stein
2006-03-15
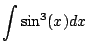
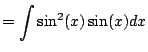
![$\displaystyle = \int [1-\cos^2(x)]\sin(x) dx$](img538.png)
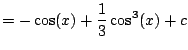 (substitution
(substitution ![$\displaystyle = \left[\frac{1-\cos(2x)}{2}\right]^2$](img544.png)
![$\displaystyle = \frac{1}{4}\cdot \left[ 1 - 2\cos(2x) + \cos^2(2x)\right]$](img545.png)
![$\displaystyle = \frac{1}{4}\left[ 1 - 2\cos(2x) + \frac{1}{2} + \frac{1}{2} \cos(4x) \right]$](img546.png)
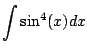
![$\displaystyle = \int \left[\frac{3}{8} - \frac{1}{2} \cos(2x) + \frac{1}{8} \cos(4x)\right] dx$](img548.png)
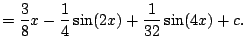
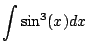
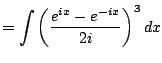
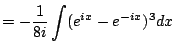
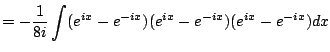
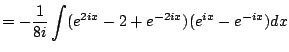
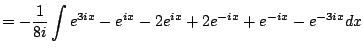
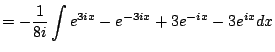
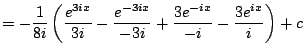
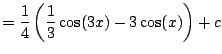
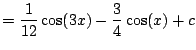
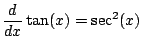
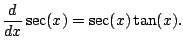

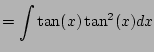
![$\displaystyle = \int \tan(x)\left[\sec^2(x) - 1\right]dx$](img567.png)
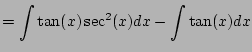
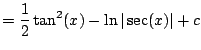
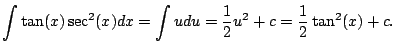
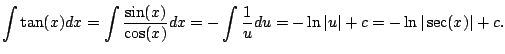
![]() as
as
![]() .
.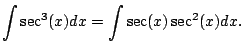
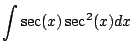
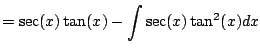
![$\displaystyle =\sec(x) \tan(x) - \int \sec(x)[\sec^2(x) - 1] dx$](img586.png)
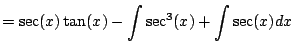
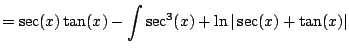
![$\displaystyle \int \sec^3(x) dx = \frac{1}{2}\Bigl[
\sec(x) \tan(x) + \ln\vert\sec(x) + \tan(x)\vert \Bigr] + c
$](img590.png)