


Next: Reading
Up: Freshman Seminar 21n: Elliptic
Previous: Introduction
Try these. If you can't do them, don't worry. That just means
we need to slow down the seminar and do more background material.
This is fine; we are in now hurry!
- (Jeff) Does the equation
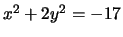 have any solutions with
have any solutions with
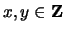 ?
?
- (Jennifer) Let
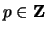 be a prime.
Prove that
be a prime.
Prove that 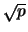 is irrational.
is irrational.
- (Mauro) Does the equation
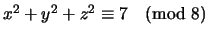 have any solutions with
have any solutions with
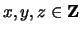 ?
?
- (Alex) Fermat's Last Theorem asserts that when
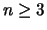 then
then
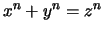 has no solutions with
has no solutions with 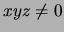 . Is the analogue
of this statement true when
. Is the analogue
of this statement true when 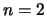 ?
?
- (Jenna) Let
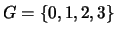 be the group of integers under addition
modulo
be the group of integers under addition
modulo 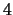 .
.
- What is
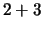 in
in 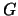 ?
?
- What is the order of
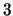 in
in 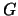 ?
?
- Let
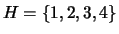 be the group of nonzero integers under multiplication
modulo
be the group of nonzero integers under multiplication
modulo 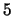 . Is
. Is 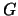 isomorphic to
isomorphic to 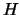 ? If not, why not? If so, give
an explicit isomorphism.
? If not, why not? If so, give
an explicit isomorphism.
- (Jeff) What is the tangent line to the graph of
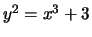 at the
point
at the
point 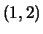 ? (Hint: Implicit differentiation.)
? (Hint: Implicit differentiation.)
- (Jennifer)
- List the elements of a finite field of order
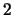 .
.
- One can prove that there is a finite field
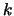 of order
of order 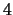 .
Does the cubic equation
.
Does the cubic equation 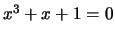 have a solution in
have a solution in 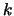 ?
?
- (Mauro)
- Prove that the set of elements of finite order
in an abelian group is a subgroup.
- Prove that a group in which every element except
the identity has order
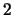 is abelian.
is abelian.
- (Alexander)
Show by example that the product of elements of finite
order in a nonabelian group need not have finite order.
(Hint: Consider a construction involving
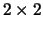 matrices.)
matrices.)
- (Jenna)
Describe all groups
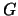 which contain no
proper subgroup.
which contain no
proper subgroup.



Next: Reading
Up: Freshman Seminar 21n: Elliptic
Previous: Introduction
William A Stein
2003-02-03
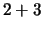 in
in 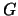 ?
?
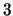 in
in 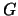 ?
?
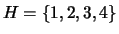 be the group of nonzero integers under multiplication
modulo
be the group of nonzero integers under multiplication
modulo 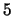 . Is
. Is 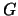 isomorphic to
isomorphic to 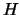 ? If not, why not? If so, give
an explicit isomorphism.
? If not, why not? If so, give
an explicit isomorphism.
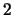 .
.
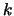 of order
of order 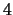 .
Does the cubic equation
.
Does the cubic equation 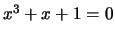 have a solution in
have a solution in 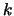 ?
?
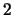 is abelian.
is abelian.