


Next: Finding large numbers that
Up: Lecture 7: Congruences, Part
Previous: How to Compute Efficiently
Recall,
Theorem 3.1
A natural number
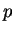
is prime if and only if
for
every
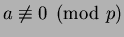
,
Thus if
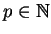 and, e.g.,
and, e.g.,
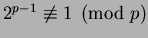 , then
we have proved that
, then
we have proved that 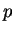 is not prime. If, however,
is not prime. If, however,
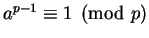 for a couple of
for a couple of 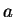 , then it is ``highly likely''
that
, then it is ``highly likely''
that 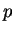 is prime. I will not analyze this probability here, but
we might later in this course.
is prime. I will not analyze this probability here, but
we might later in this course.
Example 3.2
Let
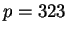
. Is
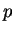
prime?
Let's compute
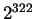
modulo
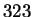
. Making a table as above, we have
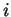 |
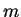 |
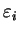 |
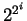 mod 323 mod 323 |
| 0 |
322 |
0 |
2 |
| 1 |
161 |
1 |
4 |
| 2 |
80 |
0 |
16 |
| 3 |
40 |
0 |
256 |
| 4 |
20 |
0 |
290 |
| 5 |
10 |
0 |
120 |
| 6 |
5 |
1 |
188 |
| 7 |
2 |
0 |
137 |
| 8 |
1 |
1 |
35 |
Thus
so
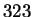
is not prime. In fact,
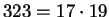
.
It's possible to prove that a large number is composite, but yet
be unable to (easily) find a factorization!
For example if
then
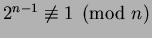 , so
, so 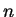 is composite.
This is something one could verify in a reasonable amount
of time by hand. (Though finding a factorization by hand
would be very difficult!)
is composite.
This is something one could verify in a reasonable amount
of time by hand. (Though finding a factorization by hand
would be very difficult!)
Subsections



Next: Finding large numbers that
Up: Lecture 7: Congruences, Part
Previous: How to Compute Efficiently
William A Stein
2001-09-25
![]() and, e.g.,
and, e.g.,
![]() , then
we have proved that
, then
we have proved that ![]() is not prime. If, however,
is not prime. If, however,
![]() for a couple of
for a couple of ![]() , then it is ``highly likely''
that
, then it is ``highly likely''
that ![]() is prime. I will not analyze this probability here, but
we might later in this course.
is prime. I will not analyze this probability here, but
we might later in this course.