Proof.
[Proof of Algorithm
1.2.3]
The part of the algorithm that is not clear is that
when the first element
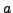
of
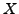
satisfies
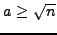
,
then each element of
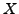
is prime.
To see this, suppose
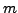
is in
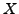
, so
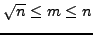
and that
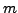
is divisible by
no prime that is
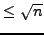
. Write
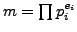
with
the
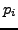
distinct primes ordered so that
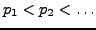
. If
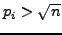
for each
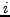
and there is more than one
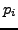
, then
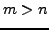
,
a contradiction. Thus some
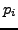
is less than
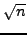
,
which also contradicts our assumptions on
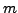
.

SAGE Example 1.2
The eratosthenes command implements the sieve in SAGE:
sage: eratosthenes(50)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]