Next: Heegner Points and Kolyvagin's Up: The -adic BSD Conjectural Previous: Example: A Curve of Contents Index
The ![]() -adic logarithm
-adic logarithm
![]() is
the unique group homomorphism with
is
the unique group homomorphism with ![]() that extends the
homomorphism
that extends the
homomorphism
![]() defined by the usual power
series of
defined by the usual power
series of ![]() about
about ![]() . Explicitly, if
. Explicitly, if
![]() , then
, then
sage: K = Qp(5,8); K 5-adic Field with capped relative precision 8 sage: a = K(-5^2*17); a 3*5^2 + 5^3 + 4*5^4 + 4*5^5 + 4*5^6 + 4*5^7 + 4*5^8 + 4*5^9 + O(5^10) sage: u = a.unit_part() 3 + 5 + 4*5^2 + 4*5^3 + 4*5^4 + 4*5^5 + 4*5^6 + 4*5^7 + O(5^8) sage: b = K(1235/5); b 2 + 4*5 + 4*5^2 + 5^3 + O(5^8) sage: log(a) 5 + 3*5^2 + 3*5^3 + 4*5^4 + 4*5^5 + 5^6 + O(5^8) sage: log(a*b) - log(a) - log(b) O(5^8)
Note that we can recover ![]() :
:
sage: c = a^b; c 2*5^494 + 4*5^496 + 2*5^497 + 5^499 + 3*5^500 + 5^501 + O(5^502) sage: log(c)/log(a) 2 + 4*5 + 4*5^2 + 5^3 + O(5^7)
Let ![]() denote the Néron model of
denote the Néron model of ![]() over
over ![]() . Let
. Let
![]() be a non-torsion point that reduces to
be a non-torsion point that reduces to
![]() and to the
connected component of
and to the
connected component of
![]() at all primes
at all primes ![]() of bad
reduction for
of bad
reduction for ![]() . For example, given any point
. For example, given any point
![]() one can construct such a
one can construct such a ![]() by multiplying it by the least common
multiple of the Tamagawa numbers of
by multiplying it by the least common
multiple of the Tamagawa numbers of ![]() .
.
sage: E = EllipticCurve('446d1')
sage: P = 3*E.gen(0); P
(32/49 : -510/343 : 1)
Let
sage: var('a1 a2 a3 a4 a6')
sage: E = EllipticCurve([a1,a2,a3,a4,a6]); E
Elliptic Curve defined by
y^2 + a1*x*y + a3*y = x^3 + a2*x^2 + a4*x + a6
over Symbolic Ring
sage: eqn = SR(E); eqn
(y^2 + a1*x*y + a3*y) == (x^3 + a2*x^2 + a4*x + a6)
sage: F = eqn.lhs() - eqn.rhs(); F
y^2 + a1*x*y + a3*y - x^3 - a2*x^2 - a4*x - a6
sage: G = w^3*F(x=t/s, y=-1/w); G.expand()
-t^3 - a2*w*t^2 - a4*w^2*t - a1*w*t - a6*w^3 - a3*w^2 + w
sage: E = EllipticCurve('37a'); E
Elliptic Curve defined by y^2 + y = x^3 - x over Rational Field
sage: F = E.formal_group(); F
Formal Group associated to the Elliptic Curve defined by
y^2 + y = x^3 - x over Rational Field
sage: x = F.x(prec=8); x
t^-2 - t + t^2 - t^4 + 2*t^5 - t^6 - 2*t^7 + O(t^8)
sage: y = F.y(prec=8); y
-t^-3 + 1 - t + t^3 - 2*t^4 + t^5 + 2*t^6 - 6*t^7 + O(t^8)
Notice that the power series satisfy the equation of the curve.
sage: y^2 + y == x^3 - x True
Recall that
![]() is the
differential on a fixed choice of Weierstrass equation for
is the
differential on a fixed choice of Weierstrass equation for
![]() . Let
. Let
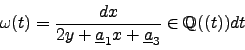
sage: F.differential(prec=8) 1 + 2*t^3 - 2*t^4 + 6*t^6 - 12*t^7 + O(t^8)
We can also compute ![]() directly from the definition:
directly from the definition:
sage: x.derivative()/(2*y+1) 1 + 2*t^3 - 2*t^4 + 6*t^6 - 12*t^7 + 6*t^8 + 20*t^9 + O(t^10)
The following theorem, which is proved in [MT91],
uniquely determines a power series
![]() and constant
and constant
![]() .
.
The above theorem produces a (very inefficient) algorithm to compute
![]() and
and ![]() . Just view
. Just view ![]() as a formal indeterminate and
compute
as a formal indeterminate and
compute
![]() , then obtain constraints on
, then obtain constraints on ![]() using that the coefficients of
using that the coefficients of ![]() must be in
must be in ![]() . These
determine
. These
determine ![]() to some precision, which increases as we compute
to some precision, which increases as we compute
![]() to higher precision. Until recently this was the only
known way to compute
to higher precision. Until recently this was the only
known way to compute ![]() and
and ![]() - fortunately the method
of [MST06] is much faster in general.
- fortunately the method
of [MST06] is much faster in general.
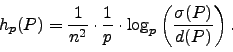
William 2007-05-25