Naive Algorithm: Compute
![]() by
repeatedly multiplying by
by
repeatedly multiplying by ![]() and reducing modulo
and reducing modulo ![]() . This is BAD
because it takes
. This is BAD
because it takes ![]() multiplications.
multiplications.
Clever Algorithm: The following observation is the key idea which
makes the clever algorithm work. Write
![]() with
each
with
each
![]() , i.e., write
, i.e., write ![]() in base
in base ![]() (binary).
Then
(binary).
Then
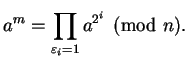
| |
|
|
|
| 0 | 91 | 1 | 6 |
| 1 | 45 | 1 | 36 |
| 2 | 22 | 0 | 96 |
| 3 | 11 | 1 | 16 |
| 4 | 5 | 1 | 56 |
| 5 | 2 | 0 | 36 |
| 6 | 1 | 1 | 96 |
Summary of above table: The first column,
labeled ![]() ,
is just to keep track of
,
is just to keep track of ![]() . The second column, labeled
. The second column, labeled ![]() ,
is got by dividing
the entry above it by
,
is got by dividing
the entry above it by ![]() and taking the integer part of the result.
The third column, labeled
and taking the integer part of the result.
The third column, labeled
![]() ,
simply records whether or not the second column is
odd. The forth column is computed by squaring, modulo 100, the entry above
it.
,
simply records whether or not the second column is
odd. The forth column is computed by squaring, modulo 100, the entry above
it.
Some examples in PARI to convince you that powering isn't too difficult:
? Mod(17,389)^5000 %13 = Mod(330, 389) ? Mod(2903,49084098)^498494 %14 = Mod(13189243, 49084098)These both take no noticeable time.