


Next: About this document ...
Homework 7: Class Groups and Elliptic Curves
DUE WEDNESDAY, NOVEMBER 14
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
- 1.
- (10 points) For any negative discriminant
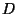 , let
, let 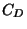 denote
the finite abelian group of equivalence classes of primitive positive
definite quadratic forms of discriminant
denote
the finite abelian group of equivalence classes of primitive positive
definite quadratic forms of discriminant 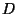 . Use the PARI program
forms.gp from lecture 24 (download it from my web page) to
compute representatives for
. Use the PARI program
forms.gp from lecture 24 (download it from my web page) to
compute representatives for 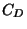 and determine the structure of
and determine the structure of 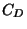 as a produce of cyclic groups for each of the following five
values of
as a produce of cyclic groups for each of the following five
values of 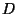 :
:
- 2.
- (6 points) Draw a beautiful graph of the set
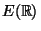 of real
points on each of the following elliptic curves:
of real
points on each of the following elliptic curves:
- (i)
-
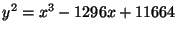 ,
,
- (ii)
-
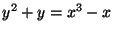 ,
,
- (iii)
-
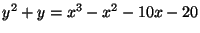 .
.
- 3.
- (4 points) A rational solution
to the equation
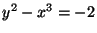 is
is 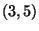 .
Find a rational solution with
.
Find a rational solution with 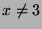 by drawing the tangent line to
by drawing the tangent line to 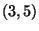 and
computing the third point of intersection.
and
computing the third point of intersection.
William A Stein
2001-11-11
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001