


Next: About this document ...
Homework 6: Binary Quadratic Forms
DUE WEDNESDAY, NOVEMBER 7
William Stein
Date: Math 124  HARVARD UNIVERSITY
HARVARD UNIVERSITY  Fall 2001
Fall 2001
There are 9 problems. Work in groups and use PARI
as much as you like.
- 1.
- (3 points)
Which of the following numbers is a sum of two
squares? Express those that are as a sum of
two squares.
- 2.
- (i)
- (4 points) Write a PARI program that takes a positive integer
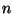 as input and outputs a sequence [x,y,z,w] of integers
such that
as input and outputs a sequence [x,y,z,w] of integers
such that
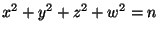 . (Hint: Your program does
not have to be efficient.)
. (Hint: Your program does
not have to be efficient.)
- (ii)
- (2 point) Write
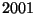 as a sum of three squares.
as a sum of three squares.
- 3.
- (3 points) Find a positive integer that has a least three different
representations as the sum of two squares, disregarding signs and
the order of the summands.
- 4.
- (5 points) Show that a natural number
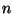 is the sum of two
integer squares if and only if it is the sum of two rational squares.
is the sum of two
integer squares if and only if it is the sum of two rational squares.
- 5.
- (6 points) Mimic the proof of the main theorem of Lecture 21 to
show that an odd prime
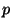 is of the form
is of the form 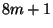 or
or 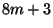 if and only
if it can be written as
if and only
if it can be written as
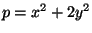 for some choice of integers
for some choice of integers 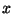 and
and 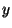 . (Hint: Use the formula for the quadratic residue symbol
. (Hint: Use the formula for the quadratic residue symbol
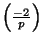 from Lecture 13.)
from Lecture 13.)
- 6.
- (4 points) A triangular number is a number that is the sum
of the first
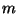 integers for some positive integer
integers for some positive integer 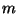 .
If
.
If 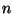 is a triangular number, show that all three of the
integers
is a triangular number, show that all three of the
integers 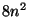 ,
, 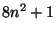 , and
, and 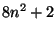 can be written as a sum of two squares.
can be written as a sum of two squares.
- 7.
- (3 points)
Prove that of any four consecutive integers, at least one is not
representable as a sum of two squares.
- 8.
- (4 points) Show that
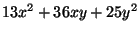 and
and
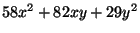 are each equivalent to the form
are each equivalent to the form
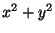 , then find integers
, then find integers 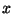 and
and 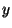 such that
such that
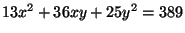 .
.
- 9.
- (4 points) What are the discriminants of the forms
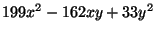 and
and
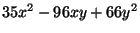 ? Are these
forms equivalent?
? Are these
forms equivalent?



Next: About this document ...
William A Stein
2001-10-31
![]() HARVARD UNIVERSITY
HARVARD UNIVERSITY ![]() Fall 2001
Fall 2001