Computing Periods¶
This chapter is about computing period maps associated to newforms. We assume you have read Chapters General Modular Symbols and Computing with Newforms and that you are familiar with abelian varieties at the level of [Ros86].
In Section The Period Map we introduce the period map and give some examples of situations in which computing it is relevant. Section Abelian Varieties Attached to Newforms is about how to use the period mapping to attach an abelian variety to any newform. In Section Extended Modular Symbols, we introduce extended modular symbols, which are the key computational tool for quickly computing periods of modular symbols. We turn to numerical computation of period integrals in Section Approximating Period Integrals, and in Section Speeding Convergence Using Atkin-Lehner we explain how to use Atkin-Lehner operators to speed convergence. In Section Computing the Period Mapping we explain how to compute the full period map with a minimum amount of work.
Section All Elliptic Curves of Given Conductor briefly sketches three approaches to computing all elliptic curves of a given conductor.
This chapter was inspired by [Cre97a], which contains
similar algorithms in the special case of a
newform 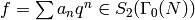 with
with 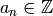 .
.
See also [Dok04] for algorithmic methods to compute
special values of very general 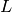 -functions, which can be used for
approximating
-functions, which can be used for
approximating 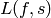 for arbitrary
for arbitrary  .
.
The Period Map¶
Let 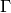 be a subgroup of
be a subgroup of 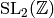 that contains
that contains
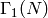 for some
for some 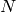 , and
suppose
, and
suppose
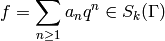
is a newform (see Definition Definition 9.9). In this chapter we describe how to approximately compute the complex period mapping
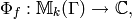
given by
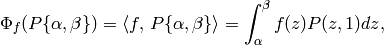
as in Section Pairing Modular Symbols and Modular Forms. As an application, we can
approximate the special values 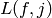 , for
, for 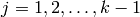 using
(?). We can also
compute the period lattice attached to a modular abelian variety,
which is an important step, e.g., in enumeration of
using
(?). We can also
compute the period lattice attached to a modular abelian variety,
which is an important step, e.g., in enumeration of
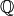 -curves (see, e.g., [GLQ04]) or computation of
a curve whose Jacobian is a modular abelian variety
-curves (see, e.g., [GLQ04]) or computation of
a curve whose Jacobian is a modular abelian variety 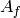 (see, e.g., [Wan95]).
(see, e.g., [Wan95]).
Abelian Varieties Attached to Newforms¶
Fix a newform 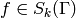 , where
, where 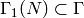 for some
for some 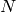 . Let
. Let 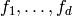 be the
be the
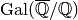 -conjugates of
-conjugates of  , where
, where 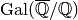 acts via
its action on the Fourier coefficients, which are algebraic integers
(since they are the eigenvalues of matrices with integer entries).
Let
acts via
its action on the Fourier coefficients, which are algebraic integers
(since they are the eigenvalues of matrices with integer entries).
Let
(1)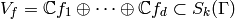
be the subspace of cusp forms spanned by the
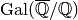 -conjugates of
-conjugates of  .
One can show using the results discussed in Section Atkin-Lehner-Li Theory
that the above sum is direct, i.e., that
.
One can show using the results discussed in Section Atkin-Lehner-Li Theory
that the above sum is direct, i.e., that 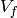 has dimension
has dimension 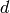 .
.
The integration pairing induces a 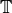 -equivariant homomorphism
-equivariant homomorphism
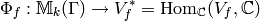
from modular symbols to the 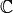 -linear dual
-linear dual 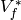 of
of 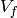 .
Here
.
Here 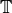 acts on
acts on 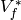 via
via 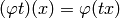 ,
and this homomorphism is
,
and this homomorphism is 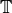 -stable by Theorem 1.42.
The abelian variety attached to
-stable by Theorem 1.42.
The abelian variety attached to  is the
quotient
is the
quotient
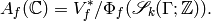
Here 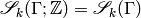 , and we include
the
, and we include
the 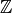 in the notation to emphasize that
these are integral modular symbols.
See [Shim59] for a proof that
in the notation to emphasize that
these are integral modular symbols.
See [Shim59] for a proof that 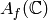 is an abelian variety (in particular,
is an abelian variety (in particular,
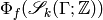 is a lattice, and
is a lattice, and
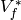 is equipped with a nondegenerate Riemann form).
is equipped with a nondegenerate Riemann form).
When 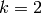 , we can also construct
, we can also construct 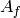 as a quotient
of the modular Jacobian
as a quotient
of the modular Jacobian 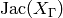 , so
, so 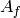 is an
abelian variety canonically defined over
is an
abelian variety canonically defined over 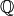 .
.
In general, we have an exact sequence
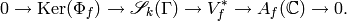
Remark 10.1
When 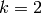 , the abelian variety
, the abelian variety 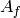 has a canonical structure of
abelian variety over
has a canonical structure of
abelian variety over 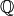 . Moreover, there is a conjecture of Ribet
and Serre in [Rib92] that describes the simple abelian
varieties
. Moreover, there is a conjecture of Ribet
and Serre in [Rib92] that describes the simple abelian
varieties 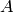 over
over 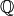 that should arise via this construction. In
particular, the conjecture is that
that should arise via this construction. In
particular, the conjecture is that 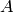 is isogenous to some abelian
variety
is isogenous to some abelian
variety 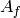 if and only if
if and only if 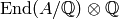 is a number field
of degree
is a number field
of degree 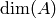 . The abelian varieties
. The abelian varieties 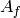 have this property
since
have this property
since 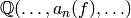 embeds in
embeds in 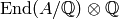 and the endomorphism ring over
and the endomorphism ring over 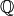 has degree at most
has degree at most 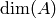 (see [Rib92] for details). Ribet proves that his
conjecture is a consequence of Serre’s conjecture
[Ser87] on modularity of mod
(see [Rib92] for details). Ribet proves that his
conjecture is a consequence of Serre’s conjecture
[Ser87] on modularity of mod 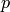 odd irreducible
Galois representations (see Section Applications of Modular Forms). Much of Serre’s
conjecture has been proved by Khare and Wintenberger (not
published). In particular, it is a theorem that if
odd irreducible
Galois representations (see Section Applications of Modular Forms). Much of Serre’s
conjecture has been proved by Khare and Wintenberger (not
published). In particular, it is a theorem that if 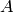 is a simple
abelian variety over
is a simple
abelian variety over 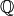 with
with 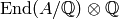 a number field
of degree
a number field
of degree 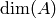 and if
and if 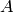 has good reduction at
has good reduction at 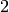 , then
, then 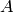 is
isogenous to some abelian variety
is
isogenous to some abelian variety 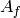 .
.
Remark 10.2
When 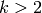 , there is an object called a
Grothendieck motive that is attached to
, there is an object called a
Grothendieck motive that is attached to  and has a canonical
“structure over
and has a canonical
“structure over 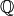 “. See [Sch90].
“. See [Sch90].
Extended Modular Symbols¶
In this section, we extend the notion of modular
symbols to allows symbols of the form
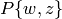 where
where 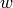 and
and  are
arbitrary elements of
are
arbitrary elements of 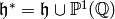 .
.
Definition 10.3
The abelian group sym{esM_k}
of extended modular symbols of weight  is the
is the 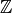 -span of symbols
-span of symbols 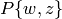 , with
, with 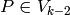 a homogeneous polynomial of degree
a homogeneous polynomial of degree 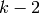 with integer
coefficients, modulo the relations
with integer
coefficients, modulo the relations
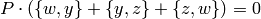
and modulo any torsion.
Fix a finite index subgroup 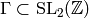 .
Just as for usual modular symbols,
.
Just as for usual modular symbols, 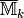 is equipped with
an action of
is equipped with
an action of 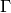 , and we
define the space of extended modular symbols of weight
, and we
define the space of extended modular symbols of weight  for
for 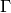 to be the quotient
to be the quotient
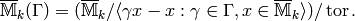
The quotient 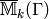 is torsion-free and fixed by
is torsion-free and fixed by 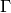 .
.
The integration pairing extends naturally to a pairing
(2)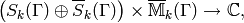
where we recall from (?) that 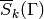 denotes
the space of antiholomorphic cusp forms.
Moreover, if
denotes
the space of antiholomorphic cusp forms.
Moreover, if
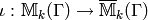
is the natural map, then  respects (2) in the sense that
for all
respects (2) in the sense that
for all 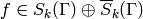 and
and 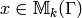 , we have
, we have
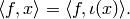
As we will see soon, it
is often useful to replace
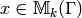 first by
first by 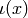 and then
by an equivalent sum
and then
by an equivalent sum 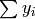 of symbols
of symbols
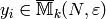 such that
such that
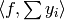 is easier to
compute numerically than
is easier to
compute numerically than 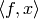 .
.
Let  be a Dirichlet character of modulus
be a Dirichlet character of modulus 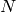 .
If
.
If 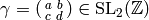 , let
, let 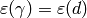 .index{
.index{ }
Let sym{esM_k(N,eps)} be the quotient of
}
Let sym{esM_k(N,eps)} be the quotient of
![\esM_k(N,\Z[\eps])](_images/math/0aaae27f21a39dae657b783b85f6bd036ec31e72.png) by the relations
by the relations 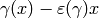 , for all
, for all ![x \in \sM_k(N,\Z[\eps])](_images/math/892898775d582cfee11afab4f1f4a74a423ecb5a.png) ,
,
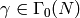 , and modulo any torsion.
, and modulo any torsion.
Approximating Period Integrals¶
In this section we assume 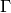 is a congruence subgroup
of
is a congruence subgroup
of 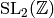 that contains
that contains 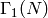 for some
for some 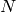 .
Suppose
.
Suppose 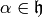 , so
, so 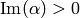 and
and 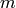 is
an integer such that
is
an integer such that 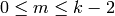 ,
and consider the extended modular symbol
,
and consider the extended modular symbol
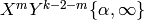 .
Let
.
Let 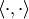 denote
the integration pairing from Section Pairing Modular Symbols and Modular Forms.
Given an arbitrary cusp form
denote
the integration pairing from Section Pairing Modular Symbols and Modular Forms.
Given an arbitrary cusp form 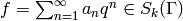 ,
we have
,
we have
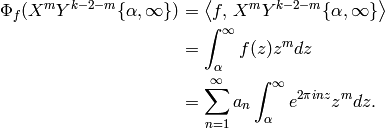
The reversal of summation and integration is justified because
the imaginary part of  is positive so that the sum
converges absolutely. The following
lemma is useful for computing the above infinite sum.
is positive so that the sum
converges absolutely. The following
lemma is useful for computing the above infinite sum.
Lemma 10.4
(3)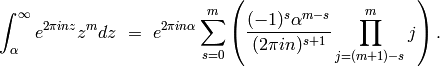
Proof
See Exercise 10.1
In practice we will usually be interested in computing the period map
 when
when  is a newform. Since
is a newform. Since  is a
newform, there is a Dirichlet character
is a
newform, there is a Dirichlet character  such that
such that 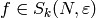 . The period map
. The period map 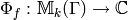 then
factors through the quotient
then
factors through the quotient 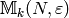 , so it suffices to
compute the period map on modular symbols in
, so it suffices to
compute the period map on modular symbols in 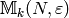 .
.
The following proposition is an analogue of [Cre97a, Prop. 2.1.1(5)].
Proposition 10.5
For any 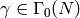 ,
, 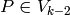 and
and 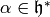 ,
we have the following relation in
,
we have the following relation in 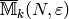 :
:
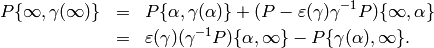
Proof
By definition, if 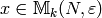 is a modular symbol
and
is a modular symbol
and 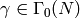 , then
, then 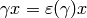 .
Thus
.
Thus 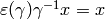 , so
, so
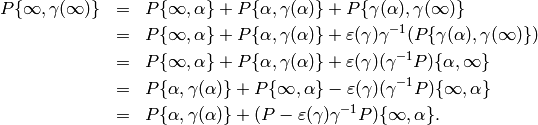
The second equality in the statement of the proposition now follows easily.
In the case of weight  and trivial character,
the “error term”
and trivial character,
the “error term”
(4)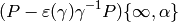
vanishes since 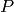 is constant and
is constant and 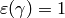 . In general this term does
not vanish. However, we can suitably modify the formulas
found in [Cre97a, 2.10] and still obtain an algorithm
for computing period integrals.
. In general this term does
not vanish. However, we can suitably modify the formulas
found in [Cre97a, 2.10] and still obtain an algorithm
for computing period integrals.
Algorithm 10.6
Given 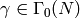 ,
, 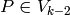 and
and
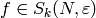 presented as a
presented as a  -expansion to some precision,
this algorithm outputs an approximation to
the period integral
-expansion to some precision,
this algorithm outputs an approximation to
the period integral
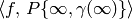 .
.
- Write
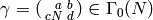 , with
, with 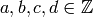 ,
and set
,
and set 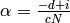 in Proposition Proposition 10.5.
in Proposition Proposition 10.5. - Replacing
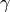 by
by 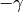 if necessary,
we find that the imaginary parts of
if necessary,
we find that the imaginary parts of 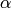 and
and
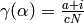 are both equal to the positive number
are both equal to the positive number 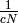 .
. - Use (?) and Lemma 10.4 to compute the integrals that appear in Proposition Proposition 10.5.
It would be nice if the modular symbols
of the form 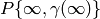 for
for 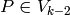 and
and
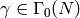 were to generate a large subspace
of
were to generate a large subspace
of 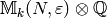 .
When
.
When 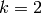 and
and 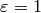 ,
Manin proved in [Man72]
that the map
,
Manin proved in [Man72]
that the map 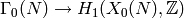 sending
sending 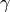 to
to 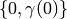 is a surjective
group homomorphism. When
is a surjective
group homomorphism. When 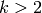 , the author
does not know a similar
group-theoretic statement. However, we have the following
theorem.
, the author
does not know a similar
group-theoretic statement. However, we have the following
theorem.
Theorem 10.7
Any element of 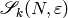 can be written in the form
can be written in the form
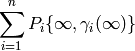
for some 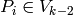 and
and 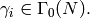 Moreover,
Moreover, 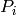 and
and 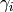 can be chosen so that
can be chosen so that
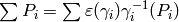 ,
so the error term (4) vanishes.
,
so the error term (4) vanishes.
Figure 10.1
“Transporting” a transportable modular symbol.
\begin{figure}
\begin{center}
\begin{picture}(230,150)(0,0)
\put(-10,10){\line(1,0){200}}
\put(10,10){\circle*{3}}
\put(10,0){`\infty`}
\qbezier(10,10)(50,40)(75,10)
\put(49,25){\vector(1,0){1}}
\put(45,28){`P`}
\put(75,10){\circle*{3}}
\put(75,0){`\gamma \infty`}
\qbezier(75,10)(130,50)(140,10)
\put(120,30){\vector(1,0){1}}
\put(115,34){`Q`}
\put(140,10){\circle*{3}}
\put(140,0){`\beta \infty`}
\put(20,90){\circle*{3}}
\put(17,96){`\alpha`}
\qbezier(20,90)(50,120)(55,60)
\put(40,100){\vector(1,0){1}}
\put(40,104){`P`}
\put(55,60){\circle*{3}}
\put(60,54){`\gamma \alpha`}
\qbezier(55,60)(70,180)(100,140)
\put(87,150){\vector(1,0){1}}
\put(85,154){`Q`}
\put(100,140){\circle*{3}}
\put(100,146){`\beta \alpha`}
\comment{
\qbezier(10,10)(-10,30)(10,50)
\qbezier(10,50)(40,70)(20,90)
\put(5,45){\vector(2,3){1}}
\qbezier(75,10)(90,30)(75,40)
\qbezier(75,40)(60,50)(55,60)
\put(69,45){\vector(1,-1){1}}
\put(80,35){\vector(-1,2){1}}
\qbezier(140,10)(160,30)(140,50)
\qbezier(140,50)(90,80)(110,90)
\qbezier(110,90)(130,100)(100,120)
\qbezier(100,120)(90,130)(100,140)
\put(110,90){\vector(-1,-1){1}}
}
\put(100,50){\vector(-1,4){10}}
\put(50,40){\vector(-1,4){10}}
\put(140,155){\parbox[t][4in][l]{2in}
{
The modular symbol
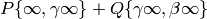
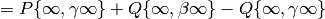
can be “transported” to
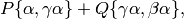
provided that
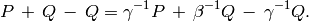
The author and Helena Verrill prove this theorem
in [SV01].
The condition
that the error term vanishes means that one can replace
 by any
by any  in the expression for the modular symbol
and obtain an equivalent modular symbol. For this reason,
we call such modular symbols transportable, as illustrated
in Figure 10.1.
in the expression for the modular symbol
and obtain an equivalent modular symbol. For this reason,
we call such modular symbols transportable, as illustrated
in Figure 10.1.
Note that in general not every element of the form
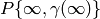 must lie in
must lie in 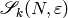 . However, if
. However, if
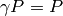 , then
, then 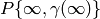 does lie in
does lie in
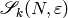 . It would be interesting to know under what
circumstances
. It would be interesting to know under what
circumstances 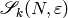 is generated by symbols of the form
is generated by symbols of the form
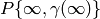 with
with 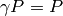 . This sometimes fails for
. This sometimes fails for
 odd; for example, when
odd; for example, when 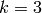 , the condition
, the condition 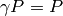 implies
that
implies
that 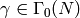 has an eigenvector with eigenvalue
has an eigenvector with eigenvalue  , and hence
is of finite order. When
, and hence
is of finite order. When  is even, the author can see no
obstruction to generating
is even, the author can see no
obstruction to generating 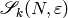 using such symbols.
using such symbols.
Speeding Convergence Using Atkin-Lehner¶
Let 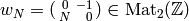 .
Consider the Atkin-Lehner involution
.
Consider the Atkin-Lehner involution 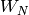 on
on 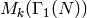 ,
which is defined by
,
which is defined by
![W_N(f) &= N^{(2-k)/2} \cdot f|_{[w_N]_k}\\
&= N^{(2-k)/2} \cdot f\left(-\frac{1}{Nz}\right) \cdot N^{k-1} \cdot (Nz)^{-k}\\
&= N^{-k/2} \cdot z^{-k} \cdot f\left(-\frac{1}{Nz}\right).](_images/math/b255460f74e49812d36f14582958ab916207278b.png)
Here we take the positive square root if  is odd.
Then
is odd.
Then 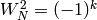 is an involution when
is an involution when  is even.
is even.
There is an operator on modular symbols, which we also denote
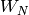 , which is given by
, which is given by
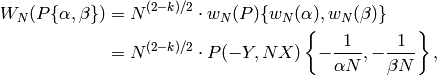
and one has that if 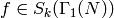 and
and 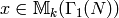 , then
, then
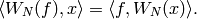
If  is a Dirichlet character of modulus
is a Dirichlet character of modulus 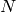 , then
the operator
, then
the operator 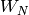 sends
sends 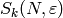 to
to
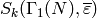 . Thus if
. Thus if 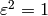 ,
then
,
then 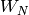 preserves
preserves 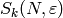 . In particular,
. In particular,
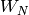 acts on
acts on 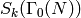 .
.
The next proposition shows how to compute the pairing
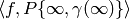 under
certain restrictive assumptions.
It generalizes a result of [Cre97b] to
higher weight.
under
certain restrictive assumptions.
It generalizes a result of [Cre97b] to
higher weight.
Proposition 10.8
Let 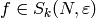 be a cusp form which is
an eigenform for the Atkin-Lehner operator
be a cusp form which is
an eigenform for the Atkin-Lehner operator 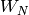 having eigenvalue
having eigenvalue 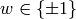 (thus
(thus 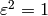 and
and  is even).
Then for any
is even).
Then for any 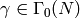 and any
and any
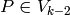 , with the property that
, with the property that 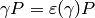 , we have
the following formula, valid for any
, we have
the following formula, valid for any 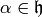 :
:
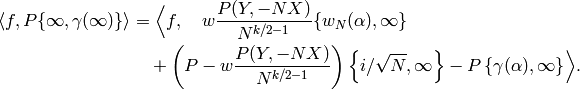
Here 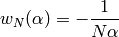 .
.
Proof
By Proposition Proposition 10.5 our condition on  implies that
implies that 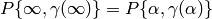 .
We describe the steps of the following computation below.
.
We describe the steps of the following computation below.
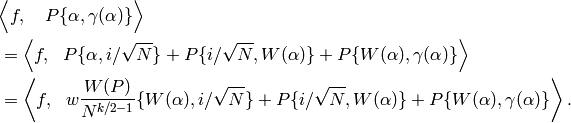
For the first equality, we break the path into three paths,
and in the second, we apply the  -involution to the first
term and use that the action of
-involution to the first
term and use that the action of  is compatible with
the pairing
is compatible with
the pairing  and that
and that  is an eigenvector
with eigenvalue
is an eigenvector
with eigenvalue 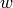 .
In the following sequence of equalities we combine the first two terms
and break up the third; then we replace
.
In the following sequence of equalities we combine the first two terms
and break up the third; then we replace 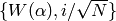 by
by
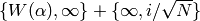 and regroup:
and regroup:
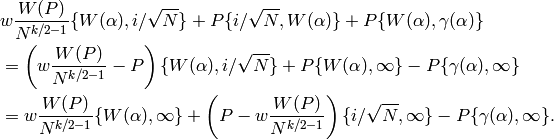
A good choice for 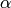 is
is
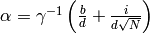 ,
so that
,
so that 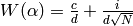 .
This maximizes the minimum of the imaginary parts
of
.
This maximizes the minimum of the imaginary parts
of 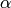 and
and 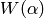 , which results in series that converge
more quickly.
, which results in series that converge
more quickly.
Let 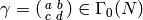 .
The polynomial
.
The polynomial
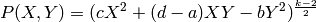
satisfies 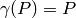 .
We obtained this formula by viewing
.
We obtained this formula by viewing 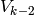 as
the
as
the 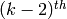 symmetric product of the
symmetric product of the 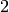 -dimensional
space on which
-dimensional
space on which 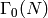 acts naturally. For example,
observe that since
acts naturally. For example,
observe that since 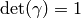 ,
the symmetric product of two eigenvectors for
,
the symmetric product of two eigenvectors for 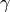 is an eigenvector
in
is an eigenvector
in 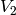 having eigenvalue
having eigenvalue  .
For the same reason, if
.
For the same reason, if 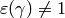 , there need
not be a polynomial
, there need
not be a polynomial 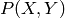 such that
such that 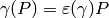 .
One remedy is to choose another
.
One remedy is to choose another 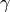 so that
so that 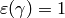 .
.
Since the imaginary parts of the terms 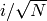 ,
, 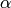 and
and
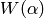 in the proposition are all relatively large, the sums
appearing at the beginning of Section Approximating Period Integrals converge
quickly if
in the proposition are all relatively large, the sums
appearing at the beginning of Section Approximating Period Integrals converge
quickly if 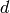 is small. It is important to
choose
is small. It is important to
choose 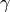 in Proposition Proposition 10.8 with
in Proposition Proposition 10.8 with 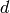 small; otherwise
the series will converge very slowly.
small; otherwise
the series will converge very slowly.
Remark 10.9
Is there a generalization of Proposition Proposition 10.8
without the restrictions that 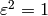 and
and  is even?
is even?
Another Atkin-Lehner Trick¶
Suppose 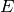 is an elliptic curve and let
is an elliptic curve and let 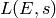 be the corresponding
be the corresponding
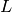 -function. Let
-function. Let 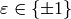 be the root number of
be the root number of 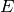 , i.e.,
the sign of the functional equation for
, i.e.,
the sign of the functional equation for 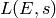 , so
, so
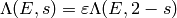 , where
, where
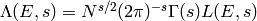 .
Let
.
Let 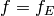 be the modular form associated to
be the modular form associated to 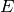 (which exists by [Wil95, BCDT01]).
If
(which exists by [Wil95, BCDT01]).
If 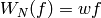 , then
, then 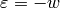 (see Exercise 10.2). We have
(see Exercise 10.2). We have
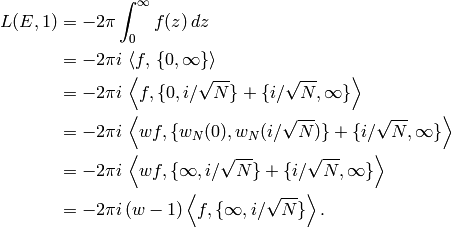
If 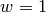 , then
, then 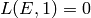 . If
. If 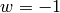 , then
, then
(5)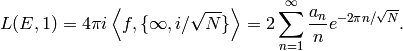
For more about computing with 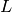 -functions of elliptic curves,
including a trick for computing
-functions of elliptic curves,
including a trick for computing  quickly without directly
computing
quickly without directly
computing 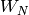 , see [Coh93, Section 7.5] and
[Cre97a, Section 2.11]. One can also find higher derivatives
, see [Coh93, Section 7.5] and
[Cre97a, Section 2.11]. One can also find higher derivatives
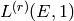 by a formula similar to (5) (see
[Cre97a, Section 2.13]). The methods in this chapter for
obtaining rapidly converging series are not just of computational
interest; see, e.g., [Gre83] for a nontrivial
theoretical application to the Birch and Swinnerton-Dyer conjecture.
by a formula similar to (5) (see
[Cre97a, Section 2.13]). The methods in this chapter for
obtaining rapidly converging series are not just of computational
interest; see, e.g., [Gre83] for a nontrivial
theoretical application to the Birch and Swinnerton-Dyer conjecture.
Computing the Period Mapping¶
Fix a newform 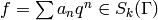 ,
where
,
where 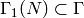 for some
for some 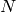 .
Let
.
Let 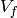 be as in (1).
be as in (1).
Let 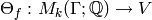 be any
be any 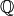 -linear map with the same kernel
as
-linear map with the same kernel
as  ; we call any such map a rational period mapping
associated to
; we call any such map a rational period mapping
associated to  . Let
. Let  be the period mapping associated
to the
be the period mapping associated
to the 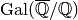 -conjugates of
-conjugates of  . We
have a commutative diagram
. We
have a commutative diagram
![\xymatrix{
{\sM_k(\Gamma;\Q)}\ar[dr]_{\Theta_f}\ar[rr]^{\Phi_f}
& & \Hom_\C(V_f,\C) \\
& V\ar@{^(->}[ur]^{i_f}
}](_images/math/7c49f38075eec0af4e770e6bd2f84eafa015ff03.png)
Recall from Section Abelian Varieties Attached to Newforms that the cokernel of
 is the abelian variety
is the abelian variety 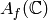 .
.
The Hecke algebra 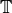 acts on the linear dual
acts on the linear dual
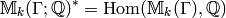
by 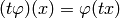 .
Let
.
Let 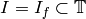 be the kernel of the
ring homomorphism
be the kernel of the
ring homomorphism ![\T\ra \Z[a_2, a_3, \ldots]](_images/math/1ccb1927f1cb8be143710be54e9978518f4c19ba.png) that sends
that sends 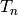 to
to 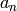 .
Let
.
Let
![\sM_k(\Gamma;\Q)^*[I] = \{\vphi \in \sM_k(\Gamma;\Q)^* : t \vphi =
0 \text{ all }t \in I\}.](_images/math/b54462247e606e9e2a16edc558aaa8e729835da4.png)
Since  is a newform, one can show that
is a newform, one can show that
![\sM_k(\Gamma;\Q)^*[I]](_images/math/f6079cc6c9d622784f6e07d328d6f7f54c80e09d.png) has dimension
has dimension 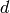 .
Let
.
Let 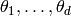 be a basis
for
be a basis
for ![\sM_k(\Gamma;\Q)^*[I]](_images/math/f6079cc6c9d622784f6e07d328d6f7f54c80e09d.png) , so
, so
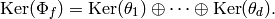
We can thus compute 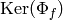 , hence a choice of
, hence a choice of 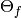 .
To compute
.
To compute  , it remains to compute
, it remains to compute 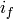 .
.
Let 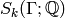 denote the space of cusp forms with
denote the space of cusp forms with
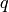 -expansion in
-expansion in ![\Q[[q]]](_images/math/59f0eca8d1174db9767b50a081db45c7b035541a.png) .
By Exercise 10.3
.
By Exercise 10.3
![S_k(\Gamma; \Q)[I] = S_k(\Gamma)[I] \cap \Q[[q]]](_images/math/73a84e91f848138fd9a6499c645b6f69bf407d2b.png)
is a 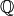 -vector space of dimension
-vector space of dimension 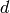 .
Let
.
Let 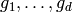 be a basis for this
be a basis for this 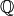 -vector space.
We will compute
-vector space.
We will compute  with respect to the basis of
with respect to the basis of
![\Hom_\Q(S_k(\Gamma;\Q)[I];\C)](_images/math/6dc90eb687d76e37c313a1cc20cea43674570d5e.png) dual to this basis.
Choose elements
dual to this basis.
Choose elements 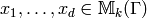 with the following properties:
with the following properties:
- Using Proposition Proposition 10.5 or Proposition Proposition 10.8,
it is possible to compute the period integrals
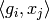 ,
, 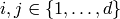 ,
efficiently.
,
efficiently. - The
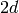 elements
elements 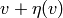 and
and 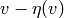 for
for 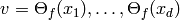 span a space of dimension
span a space of dimension 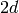 (i.e., they span
(i.e., they span 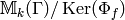 ).
).
Given this data, we can compute
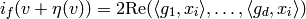
and
We break the integrals into real and imaginary parts because this
increases the precision of our answers.
Since the vectors 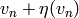 and
and 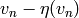 ,
, 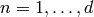 , span
, span
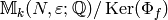 , we have computed
, we have computed 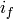 .
.
Remark 10.10
We want to find symbols 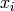 satisfying the
conditions of Proposition Proposition 10.8. This is usually possible
when
satisfying the
conditions of Proposition Proposition 10.8. This is usually possible
when 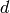 is very small, but in practice it is difficult when
is very small, but in practice it is difficult when 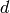 is large.
is large.
Remark 10.11
The above strategy was motivated by [Cre97a, Section 2.10].
All Elliptic Curves of Given Conductor¶
Using modular symbols and the period map, we can compute all elliptic
curves over 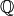 of conductor
of conductor 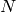 , up to isogeny. The algorithm in
this section gives all modular elliptic curves (up to isogeny),
i.e., elliptic curves attached to modular forms, of conductor
, up to isogeny. The algorithm in
this section gives all modular elliptic curves (up to isogeny),
i.e., elliptic curves attached to modular forms, of conductor 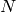 .
Fortunately, it is now known by
[Wil95, BCDT01, TW95]
that every
elliptic curve over
.
Fortunately, it is now known by
[Wil95, BCDT01, TW95]
that every
elliptic curve over 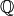 is modular, so the procedure of this section
gives all elliptic curves (up to isogeny) of given conductor. See
[Cre06] for a nice historical discussion of this
problem.
is modular, so the procedure of this section
gives all elliptic curves (up to isogeny) of given conductor. See
[Cre06] for a nice historical discussion of this
problem.
Algorithm 10.12
Given 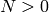 , this
algorithm outputs equations for all
elliptic curves of conductor
, this
algorithm outputs equations for all
elliptic curves of conductor 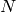 , up to isogeny.
, up to isogeny.
[Modular Symbols] Compute
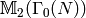 using Section Explicitly Computing .
using Section Explicitly Computing .[Find Rational Eigenspaces] Find the
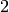 -dimensional eigenspaces
-dimensional eigenspaces 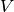 in
in
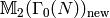 that correspond to elliptic curves.
Do not use the algorithm for decomposition from
Section Decomposing Spaces under the Action of Matrix, which is too complicated
and gives more information than we need. Instead, for the first
few primes
that correspond to elliptic curves.
Do not use the algorithm for decomposition from
Section Decomposing Spaces under the Action of Matrix, which is too complicated
and gives more information than we need. Instead, for the first
few primes 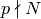 , compute all eigenspaces
, compute all eigenspaces 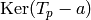 , where
, where
 runs through integers with
runs through integers with 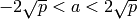 .
Intersect these eigenspaces to find the eigenspaces that
correspond to elliptic curves. To find just the new ones,
either compute the degeneracy maps to lower level or find
all the rational eigenspaces of all levels that strictly
divide
.
Intersect these eigenspaces to find the eigenspaces that
correspond to elliptic curves. To find just the new ones,
either compute the degeneracy maps to lower level or find
all the rational eigenspaces of all levels that strictly
divide 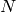 and exclude them.
and exclude them.[Find Newforms] Use Algorithm 9.14 to compute to some precision each newform
![f=\sum_{n=1}^{\infty} a_n q^n \in \Z[[q]]](_images/math/e47ac17aa654a62780a66740ace793fdf4389e20.png) associated
to each eigenspace
associated
to each eigenspace 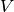 found in step (2).
found in step (2).[Find Each Curve] For each newform
 found in step (3), do the following:
found in step (3), do the following:[Period Lattice] Compute the corresponding period lattice
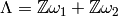 by computing the image of
by computing the image of  ,
as described in Section Computing the Period Mapping.
,
as described in Section Computing the Period Mapping.[Compute
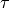 ]
Let
]
Let 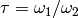 . If
. If 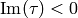 , swap
, swap
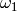 and
and 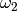 , so
, so 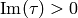 .
By successively applying generators of
.
By successively applying generators of 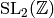 ,
we find an
,
we find an 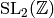 equivalent element
equivalent element 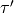 in
in 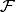 , i.e.,
, i.e.,
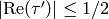 and
and 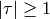 .
.[
 -invariants] Compute the invariants
-invariants] Compute the invariants 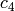 and
and 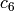 of the lattice
of the lattice 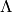 using the following
rapidly convergent series:
using the following
rapidly convergent series: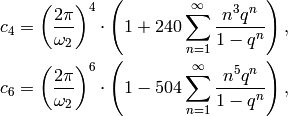
where
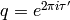 , where
, where 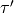 is as in step
(b).
A theorem of Edixhoven
(that the Manin constant is an integer) implies that
the invariants
is as in step
(b).
A theorem of Edixhoven
(that the Manin constant is an integer) implies that
the invariants 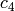 and
and 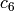 of
of 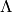 are integers,
so it is only necessary to compute
are integers,
so it is only necessary to compute 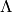 to large
precision to completely determine them.
to large
precision to completely determine them.[Elliptic Curve] An elliptic curve with invariants
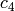 and
and 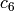 is
is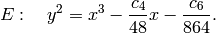
[Prove Correctness] Using Tate’s algorithm, find the conductor of
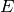 . If the conductor is not
. If the conductor is not 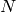 , then recompute
, then recompute 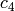 and
and
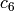 using more terms of
using more terms of  and real numbers
to larger precision, etc. If the conductor is
and real numbers
to larger precision, etc. If the conductor is 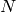 ,
compute the coefficients
,
compute the coefficients 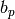 of the modular form
of the modular form 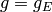 attached to the elliptic curve
attached to the elliptic curve 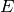 , for
, for 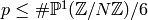 .
Verify that
.
Verify that 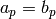 , where
, where 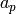 are the coefficients
of
are the coefficients
of  . If this equality holds, then
. If this equality holds, then 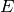 must be isogenous
to the elliptic curve attached to
must be isogenous
to the elliptic curve attached to  , by the Sturm
bound (Theorem 9.18) and Faltings’s isogeny theorem.
If the equality fails for some
, by the Sturm
bound (Theorem 9.18) and Faltings’s isogeny theorem.
If the equality fails for some 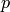 , recompute
, recompute 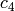 and
and 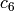 to larger precision.
to larger precision.
There are numerous tricks to optimize the above algorithm.
For example, often one can work separately with
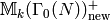 and
and
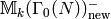 and
get enough information to find
and
get enough information to find 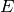 , up to isogeny
(see [Cre97b]).
, up to isogeny
(see [Cre97b]).
Once we have one curve from each isogeny class of curves of
conductor 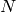 , we find each curve in each isogeny class (which is
another interesting problem discussed in [Cre97a]), hence
all curves of conductor
, we find each curve in each isogeny class (which is
another interesting problem discussed in [Cre97a]), hence
all curves of conductor 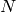 . If
. If 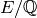 is an elliptic curve, then any
curve isogenous to
is an elliptic curve, then any
curve isogenous to 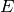 is isogenous via a chain of isogenies of prime
degree. There is an a priori bound on the degrees of these
isogenies due to Mazur. Also, there are various methods for finding
all isogenies of a given degree with domain
is isogenous via a chain of isogenies of prime
degree. There is an a priori bound on the degrees of these
isogenies due to Mazur. Also, there are various methods for finding
all isogenies of a given degree with domain 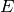 . See
[Cre97a, Section 3.8] for more details.
. See
[Cre97a, Section 3.8] for more details.
Finding Curves: 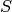 -Integral Points¶
-Integral Points¶
In this section we briefly survey an alternative approach to finding curves of a given conductor by finding integral points on other elliptic curves.
Cremona and others have developed a complementary
approach to the problem of computing all elliptic curves of given
conductor (see [CL04]). Instead of computing all
curves of given conductor, we instead consider the seemingly more
difficult problem of finding all curves with good reduction outside a
finite set 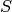 of primes. Since one can compute the conductor of a
curve using Tate’s algorithm
[Tat75, Cre97a, Section 3.2],
if we know all curves with good reduction
outside
of primes. Since one can compute the conductor of a
curve using Tate’s algorithm
[Tat75, Cre97a, Section 3.2],
if we know all curves with good reduction
outside 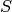 , we can find all curves of conductor
, we can find all curves of conductor 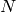 by letting
by letting 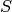 be
the set of prime divisors of
be
the set of prime divisors of 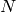 .
.
There is a strategy for finding all curves with good reduction
outside 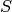 . It is not an algorithm, in the sense
that it is always guaranteed to terminate (the modular symbols method
above is an algorithm), but in practice it often works. Also,
this strategy makes sense over any number field, whereas the modular
symbols method does not (there are generalizations of modular
symbols to other number fields).
. It is not an algorithm, in the sense
that it is always guaranteed to terminate (the modular symbols method
above is an algorithm), but in practice it often works. Also,
this strategy makes sense over any number field, whereas the modular
symbols method does not (there are generalizations of modular
symbols to other number fields).
Fix a finite set 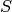 of primes of a number field
of primes of a number field 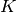 . It is a theorem
of Shafarevich that there are only finitely many elliptic curves with
good reduction outside
. It is a theorem
of Shafarevich that there are only finitely many elliptic curves with
good reduction outside 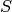 (see [Sil82, Section IX.6]). His
proof uses that the group of
(see [Sil82, Section IX.6]). His
proof uses that the group of 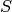 -units in
-units in 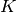 is finite and Siegel’s
theorem that there are only finitely many
is finite and Siegel’s
theorem that there are only finitely many 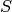 -integral points on an
elliptic curve. One can make all this explicit, and sometimes in
practice one can compute all these
-integral points on an
elliptic curve. One can make all this explicit, and sometimes in
practice one can compute all these 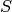 -integral points.
-integral points.
The problem of finding all elliptic curves with good reduction outside
of 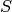 can be broken into several subproblems, the main ones being
can be broken into several subproblems, the main ones being
determine the following finite subgroup of
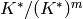 :
: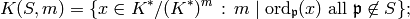
find all
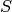 -integral points on certain elliptic curves
-integral points on certain elliptic curves
 .
.
In [CL04], there is one example, where they find all
curves of conductor 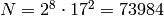 by finding all curves
with good reduction outside
by finding all curves
with good reduction outside 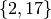 . They finds
. They finds 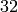 curves of
conductor
curves of
conductor 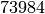 that divide into
that divide into 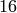 isogeny classes.
(Note that
isogeny classes.
(Note that 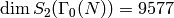 .)
.)
Finding Curves: Enumeration¶
One can also find curves by simply enumerating Weierstrass equations.
For example, the paper [SW02] discusses a database
that the author and Watkins created that contains hundreds of millions
of elliptic curves. It was constructed by enumerating Weierstrass
equations of a certain form. This database does not contain
every curve of each conductor included in the database. It is,
however, fairly complete in some cases. For example, using the Mestre
method of graphs [Mes86], we verified in [JBS03] that
the database contains all elliptic curve of prime conductor 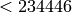 , which implies that the smallest conductor
rank
, which implies that the smallest conductor
rank 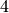 curve is composite.
curve is composite.
Exercises¶
Exercise 10.1
Prove Lemma 10.4.
Exercise 10.2
Suppose 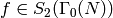 is a newform
and that
is a newform
and that 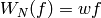 . Let
. Let 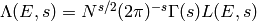 .
Prove that
.
Prove that
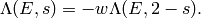
[Hint: Show that 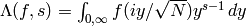 .
Then substitute
.
Then substitute 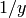 for
for 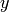 .]
.]
Exercise 10.3
Let ![f=\sum a_n q^n \in \C[[q]]](_images/math/fa1649af4150949bd79efb718570d0a9c26b7045.png) be a power
series whose coefficients
be a power
series whose coefficients 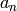 together generate a number field
together generate a number field 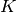 of
degree
of
degree 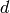 over
over 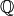 . Let
. Let 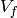 be the complex vector space spanned
by the
be the complex vector space spanned
by the 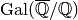 -conjugates of
-conjugates of  .
.
- Give an example to show that
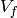 need not have dimension
need not have dimension 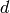 .
. - Suppose
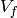 has dimension
has dimension 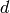 . Prove that
. Prove that ![V_f \cap
\Q[[q]]](_images/math/b67bd75f7079035a09a8e8f97b683787f619bc1c.png) is a
is a 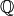 -vector space of dimension
-vector space of dimension 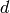 .
.
Exercise 10.4
Find an elliptic curve of conductor 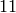 using Section
All Elliptic Curves of Given Conductor.
using Section
All Elliptic Curves of Given Conductor.