


Next: Bibliography
Up: Parity structures and generating
Previous: The ideal and the
We now give a generalization of the notion of parity structures,
and we discuss some of our results above that can be extended to this
situation. In order to motivate our generalization, we note that a
subset T of the power set of S is a parity structure if and only
if for every subset b of S, the product
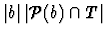 is even.
is even.
Let m be a positive integer, S be a finite set, and T be a
multiset whose elements are subsets of S, each having a multiplicity
less than m. We say that T is a mod-m parity
multistructure for S if, for each subset b of S, the number m
divides
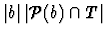 ,
where, in this intersection,
each subset of b is counted as many times as it occurs in T.
If T actually is a set (that is, has all multiplicities at most 1),
then we say that it is a mod-m parity structure.
,
where, in this intersection,
each subset of b is counted as many times as it occurs in T.
If T actually is a set (that is, has all multiplicities at most 1),
then we say that it is a mod-m parity structure.
In order to understand mod-m parity multistructures, we use the ring
We define a map 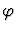 from the collection of multisets of subsets
of S to RS,m just as before, by sending a subset a of S
to
from the collection of multisets of subsets
of S to RS,m just as before, by sending a subset a of S
to
 and extending linearly.
In this ring RS,m we define
and extending linearly.
In this ring RS,m we define 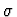 to be
to be
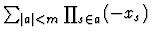 .
Notice that both of
these definitions agree with our earlier ones in the case where m
is 2. As in the proof of Theorem 1, we can show
that the images under
.
Notice that both of
these definitions agree with our earlier ones in the case where m
is 2. As in the proof of Theorem 1, we can show
that the images under 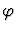 of mod-m parity multistructures form
the ideal
of mod-m parity multistructures form
the ideal
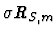 .
If S has size n, then,
as in Corollary 1, there will be a total
of
.
If S has size n, then,
as in Corollary 1, there will be a total
of
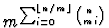 mod-m parity multistructures. However, as we lack the automorphism
of RS interchanging the ideals corresponding to I and J from
the proof of Theorem 1, we do not obtain a
formula as simple as the one from that theorem.
mod-m parity multistructures. However, as we lack the automorphism
of RS interchanging the ideals corresponding to I and J from
the proof of Theorem 1, we do not obtain a
formula as simple as the one from that theorem.
We can also generalize Theorem 2 and
Corollary 2. Again, the proofs are similar to the ones we
have for parity structures, but for the second, there is a bit of
calculation with binomial coefficients.
Theorem 3
For every mod-m parity multistructure T for a finite set S
and every subset b of S of size divisible by m, the number of
subsets of b of size relatively prime to m that lie in T is a
multiple of m.
For a collection T of subsets of a finite set S and a sequence of
natural numbers
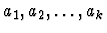 ,
write
,
write
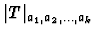 for the number of elements
of T having size equal to ai for some value of i.
for the number of elements
of T having size equal to ai for some value of i.
Theorem 4
Let
T be a mod-
m parity multistructure for a finite set
S.
- a)
- For any subset b of S and any multiple k of m, the number m
divides
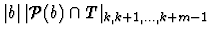 .
.
- b)
- For any subset b of S of size divisible by m and any natural
number k, the number m divides
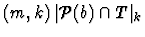 ,
where (m,k) is the greatest common divisor of m and k.
,
where (m,k) is the greatest common divisor of m and k.
It is harder, on the other hand, to understand mod-m parity structures.
We know of two basic families: For any subset c of S of size
congruent to 1 modulo m, the collection of subsets of S obtained
by adding m-1 new elements to c forms a mod-m parity structure.
And for any subset c of S of size congruent to 2 modulo m,
the collection of subsets of S obtained by adding either m-2
or m-1 new elements to c forms a mod-m parity structure.
Of course, any disjoint unions of collections of the above types will
also be mod-m parity structures, but for m greater than 2,
these are the only examples we know. It would be nice to know
whether there are more, and we pose the following open problem:
Question 1
How many mod-m parity structures are there on a set of size n?



Next: Bibliography
Up: Parity structures and generating
Previous: The ideal and the
William Arthur Stein
1999-10-27
![]() ,
where, in this intersection,
each subset of b is counted as many times as it occurs in T.
If T actually is a set (that is, has all multiplicities at most 1),
then we say that it is a mod-m parity structure.
,
where, in this intersection,
each subset of b is counted as many times as it occurs in T.
If T actually is a set (that is, has all multiplicities at most 1),
then we say that it is a mod-m parity structure.
![\begin{displaymath}R_{S,m}
:= \frac{{\bf Z}/m{\bf Z}[x_{s}\, :\, s \in S]}{(x_{s}^{2}- x_{s}\, :
\, s \in S)}.
\end{displaymath}](img47.gif)
![]() ,
write
,
write
![]() for the number of elements
of T having size equal to ai for some value of i.
for the number of elements
of T having size equal to ai for some value of i.