Bibliography

ABC⁺

B. Allombert, K. Belabas, H. Cohen, X. Roblot, and I. Zakharevitch, PARI/GP, http://pari.math.u-bordeaux.fr/.

Art59

E. Artin, Theory of algebraic numbers, Notes by Gerhard Würges from lectures held at the Mathematisches Institut, Göttingen, Germany, in the Winter Semester, vol. 1956/7, George Striker, Schildweg 12, Göttingen, 1959.

Art91

M. Artin, Algebra, Prentice Hall Inc., Englewood Cliffs, NJ, 1991.

AT90

E. Artin and J. Tate, Class field theory, second ed., Advanced Book Classics, Addison-Wesley Publishing Company Advanced Book Program, Redwood City, CA, 1990.

BCP97

W. Bosma, J. Cannon, and C. Playoust, The Magma algebra system. I. The user language, J. Symbolic Comput. 24 (1997), no. 3-4, 235-265, Computational algebra and number theory (London, 1993).

Cas67

J.W.S. Cassels, Global fields, Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), Thompson, Washington, D.C., 1967, pp. 42-84.

Cas91

to3em, Lectures on elliptic curves, London Mathematical Society Student Texts, vol. 24, Cambridge University Press, Cambridge, 1991.

Coh93

H. Cohen, A course in computational algebraic number theory, Springer-Verlag, Berlin, 1993.

Cp86

J.W.S. Cassels and A. Fröhlich (eds.), Algebraic number theory, London, Academic Press Inc. [Harcourt Brace Jovanovich Publishers], 1986, Reprint of the 1967 original.

EH00

D. Eisenbud and J. Harris, The geometry of schemes, Springer-Verlag, New York, 2000.

Fre94

G. Frey (ed.), On Artin's conjecture for odd 2-dimensional representations, Springer-Verlag, Berlin, 1994, 1585.

Iwa53

K. Iwasawa, On the rings of valuation vectors, Ann. of Math. (2) 57 (1953), 331-356.

Lan64

S. Lang, Algebraic numbers, Addison-Wesley Publishing Co., Inc., Reading, Mass.-Palo Alto-London, 1964.

Lan80

R.P. Langlands, Base change for 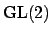${\rm {G}{L}}(2)$, Princeton University Press, Princeton, N.J., 1980.

Len02

H.W. Lenstra, Jr., Solving the Pell equation, Notices Amer. Math. Soc. 49 (2002), no. 2, 182-192.

LL93

A.K. Lenstra and H.W. Lenstra, Jr. (eds.), The development of the number field sieve, Springer-Verlag, Berlin, 1993.

Mah64

K. Mahler, Inequalities for ideal bases in algebraic number fields, J. Austral. Math. Soc. 4 (1964), 425-448.

SD01

H.P.F. Swinnerton-Dyer, A brief guide to algebraic number theory, London Mathematical Society Student Texts, vol. 50, Cambridge University Press, Cambridge, 2001.

Ser73

J-P. Serre, A Course in Arithmetic, Springer-Verlag, New York, 1973, Translated from the French, Graduate Texts in Mathematics, No. 7.

Wei82

A. Weil, Adeles and algebraic groups, Progress in Mathematics, vol. 23, Birkhäuser Boston, Mass., 1982, With appendices by M. Demazure and Takashi Ono.