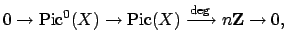For those familiar with algebraic geometry and algebraic curves, one
can prove Theorem 21.2.3 from an alternative point of
view. There is a bijection between nonsingular geometrically
irreducible projective curves over
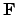 and function fields
and function fields  over
over
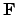 (which we assume are finite separable extensions of
(which we assume are finite separable extensions of
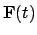 such
that
such
that
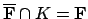 ). Let
). Let 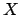 be the curve corresponding to
be the curve corresponding to  .
The group
.
The group 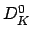 is in bijection with the divisors of degree 0 on
is in bijection with the divisors of degree 0 on
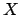 , a group typically denoted
, a group typically denoted
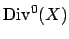 . The quotient of
. The quotient of
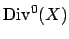 by principal divisors is denoted
by principal divisors is denoted
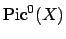 . The Jacobian of
. The Jacobian of 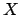 is an abelian variety
is an abelian variety
 over the finite
field
over the finite
field
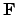 whose dimension is equal to the genus of
whose dimension is equal to the genus of 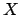 . Moreover,
assuming
. Moreover,
assuming 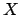 has an
has an
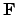 -rational point, the elements of
-rational point, the elements of
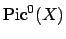 are in natural bijection with the
are in natural bijection with the
 -rational points on
-rational points on 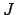 . In
particular, with these hypothesis, the class group of
. In
particular, with these hypothesis, the class group of  , which is
isomorphic to
, which is
isomorphic to
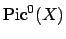 , is in bijection with the group of
, is in bijection with the group of
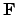 -rational points on an algebraic variety over a finite field.
This gives an alternative more complicated proof of finiteness of the
degree 0 class group of a function field.
-rational points on an algebraic variety over a finite field.
This gives an alternative more complicated proof of finiteness of the
degree 0 class group of a function field.
Without the degree 0 condition, the divisor class group won't be finite. It
is an extension of
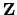 by a finite group.
by a finite group.
where 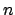 is the greatest common divisor of the degrees of
elements of
is the greatest common divisor of the degrees of
elements of 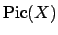 , which is
, which is 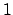 when
when 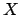 has a rational
point.
has a rational
point.
William Stein
2004-05-06
![]() by a finite group.
by a finite group.