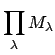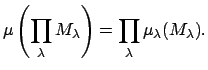In this section we describe a topological tool, which we need in order
to define adeles (see Definition 20.3.1).
Definition 20.2.1 (Restricted Topological Products)
Let
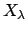
, for
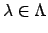
, be a family of topological
spaces, and for almost all
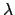
let
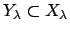
be an open subset of
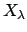
. Consider the space
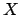
whose elements are sequences
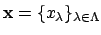
, where
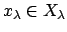
for every
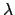
, and
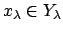
for almost all
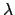
. We give
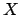
a
topology by taking as a basis of open sets the sets
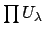
, where
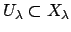
is open for all
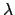
, and
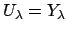
for almost all
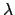
.
We call
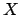
with this topology the
of the
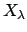
with respect to the
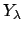
.
The restricted topological product depends on the totality of the
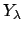 , but not on the individual
, but not on the individual
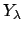 :
:
Lemma 20.2.3
Let
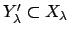 be open subsets, and suppose
that
be open subsets, and suppose
that
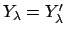 for almost all
for almost all 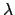 . Then
the restricted topological product of the
. Then
the restricted topological product of the 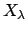 with respect
to the
with respect
to the
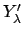 is canonically isomorphic to the restricted
topological product with respect to the
is canonically isomorphic to the restricted
topological product with respect to the
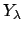 .
.
Lemma 20.2.4
Suppose that the 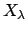 are locally compact and that the
are locally compact and that the
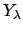 are compact. Then the restricted topological
product
are compact. Then the restricted topological
product 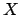 of the
of the 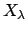 is locally compact.
is locally compact.
Proof.
For any finite subset
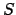
of
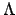
, the open subset
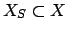
is locally compact, because by Lemma
20.2.2 it is a product
of finitely many locally compact sets with an infinite product of
compact sets. (Here we are using Tychonoff's theorem from topology,
which asserts that an arbitrary product of compact topological
spaces is compact (see Munkres's
Topology, a first course,
chapter 5).) Since
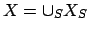
, and the
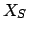
are open in
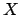
,
the result follows.

The following measure will be extremely important in deducing
topological properties of the ideles, which will be used in
proving finiteness of class groups. See, e.g., the
proof of Lemma 20.4.1, which is a key input
to the proof of strong approximation (Theorem 20.4.4).
Definition 20.2.5 (Product Measure)
For all
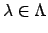
, suppose
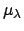
is a measure on
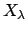
with
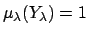
when
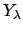
is
defined. We define the
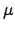
on
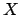
to be
that for which a basis of measurable sets is
where each
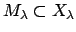
has finite
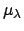
-measure and
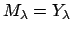
for almost all
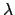
, and where
William Stein
2004-05-06
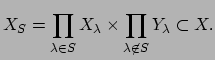
![]() , but not on the individual
, but not on the individual
![]() :
: