Suppose 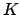 is a number field that is Galois over
is a number field that is Galois over
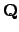 with
group
with
group
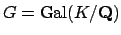 .
Fix a prime
.
Fix a prime
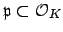 lying over
lying over
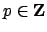 .
.
(Note: The decomposition group is called the ``splitting group''
in Swinnerton-Dyer. Everybody I know calls it the decomposition
group, so we will too.)
Let
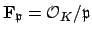 denote the residue class field of
denote the residue class field of
 .
In this section we will prove that there is a natural exact sequence
.
In this section we will prove that there is a natural exact sequence
where
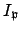 is the of
is the of
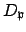 , and
, and
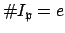 . The most interesting part of the proof is
showing that the natural map
. The most interesting part of the proof is
showing that the natural map
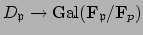 is surjective.
is surjective.
We will also discuss the structure of
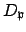 and introduce
Frobenius elements, which play a crucial roll in understanding Galois
representations.
and introduce
Frobenius elements, which play a crucial roll in understanding Galois
representations.
Recall that 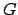 acts on the set of primes
acts on the set of primes
 lying
over
lying
over 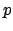 . Thus the decomposition group is the stabilizer in
. Thus the decomposition group is the stabilizer in 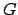 of
of
 . The orbit-stabilizer theorem implies that
. The orbit-stabilizer theorem implies that
![$ [G:D_\mathfrak{p}]$](img1285.png) equals the orbit of
equals the orbit of
 , which by Theorem 13.2.2
equals the number
, which by Theorem 13.2.2
equals the number 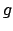 of primes lying over
of primes lying over 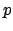 , so
, so
![$ [G:D_\mathfrak{p}]=g$](img1286.png) .
.
Lemma 14.1.2
The decomposition subgroups
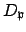 corresponding to primes
corresponding to primes
 lying over a given
lying over a given 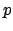 are all conjugate in
are all conjugate in 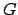 .
.
Proof.
We have
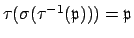
if and only if
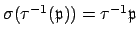
. Thus
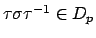
if and only if
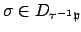
, so
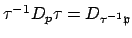
. The lemma now follows
because, by Theorem
13.2.2,
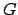
acts transitively on the set of

lying over
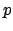
.

The decomposition group is extremely useful because it allows us
to see the extension
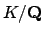 as a tower of extensions, such that at
each step in the tower we understand well the splitting behavior
of the primes lying over
as a tower of extensions, such that at
each step in the tower we understand well the splitting behavior
of the primes lying over 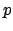 . Now might be a good time to glance
ahead at Figure 14.1.2 on page
. Now might be a good time to glance
ahead at Figure 14.1.2 on page ![[*]](/usr/share/latex2html/icons/crossref.png) .
.
We characterize the fixed field of
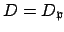 as follows.
as follows.
Proof.
First suppose
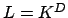
, and note that by Galois theory
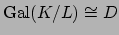
, and by Theorem
13.2.2, the group
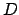
acts transitively on the primes of
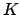
lying over
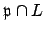
. One of
these primes is

, and
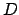
fixes

by definition, so there is
only one prime of
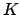
lying over
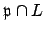
, i.e.,
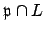
does not
split in
. Conversely, if
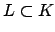
is such that
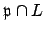
does not split in
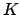
, then
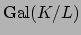
fixes

(since it is the only
prime over
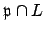
), so
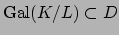
, hence
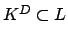
.

Thus 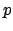 does not split in going from
does not split in going from 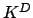 to
to 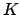 --it does some
combination of ramifying and staying inert. To fill in more of
the picture, the following proposition asserts that
--it does some
combination of ramifying and staying inert. To fill in more of
the picture, the following proposition asserts that 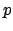 splits
completely and does not ramify in
splits
completely and does not ramify in
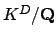 .
.
Proposition 14.1.4
Let 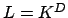 for our fixed prime
for our fixed prime 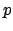 and Galois extension
and Galois extension
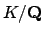 .
Let
.
Let
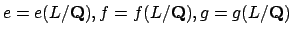 be for
be for
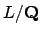 and
and 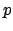 .
Then
.
Then 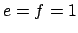 and
and
![$ g=[L:\mathbf{Q}]$](img1307.png) , i.e.,
, i.e., 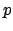 does not ramify and splits
completely in
does not ramify and splits
completely in 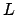 . Also
. Also
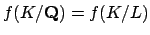 and
and
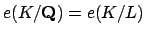 .
.
Proof.
As mentioned right after Definition
14.1.1, the
orbit-stabilizer theorem implies that
![$ g(K/\mathbf{Q})=[G:D]$](img1310.png)
, and
by Galois theory
![$ [G:D]=[L:\mathbf{Q}]$](img1311.png)
.
Thus
Now
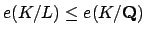
and
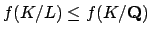
, so
we must have
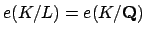
and
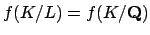
.
Since
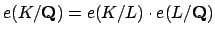
and
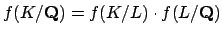
,
the proposition follows.

Subsections
William Stein
2004-05-06
![]() denote the residue class field of
denote the residue class field of
![]() .
In this section we will prove that there is a natural exact sequence
.
In this section we will prove that there is a natural exact sequence
![]() and introduce
Frobenius elements, which play a crucial roll in understanding Galois
representations.
and introduce
Frobenius elements, which play a crucial roll in understanding Galois
representations.
![]() acts on the set of primes
acts on the set of primes
![]() lying
over
lying
over ![]() . Thus the decomposition group is the stabilizer in
. Thus the decomposition group is the stabilizer in ![]() of
of
![]() . The orbit-stabilizer theorem implies that
. The orbit-stabilizer theorem implies that
![]() equals the orbit of
equals the orbit of
![]() , which by Theorem 13.2.2
equals the number
, which by Theorem 13.2.2
equals the number ![]() of primes lying over
of primes lying over ![]() , so
, so
![]() .
.
![]() as a tower of extensions, such that at
each step in the tower we understand well the splitting behavior
of the primes lying over
as a tower of extensions, such that at
each step in the tower we understand well the splitting behavior
of the primes lying over ![]() . Now might be a good time to glance
ahead at Figure 14.1.2 on page
. Now might be a good time to glance
ahead at Figure 14.1.2 on page ![]() .
.
![]() as follows.
as follows.
![$\displaystyle = \frac{e(K/\mathbf{Q})\cdot f(K/\mathbf{Q}) \cdot g(K/\mathbf{Q})}{[L:\mathbf{Q}]} = e(K/\mathbf{Q})\cdot f(K/\mathbf{Q}).$](img1314.png)