Fix an algebraic closure
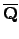 of
of
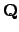 . For example,
. For example,
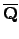 could
be the subfield of the complex numbers
could
be the subfield of the complex numbers
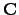 generated by all roots in
generated by all roots in
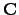 of all polynomials with coefficients in
of all polynomials with coefficients in
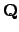 .
.
Much of this course is about algebraic integers.
Definition 5.1.1 (Algebraic Integer)
An element
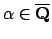
is an
if it is a
root of some monic polynomial with coefficients in

.
Definition 5.1.2 (Minimal Polynomial)
The
of
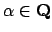
is the monic polynomial
![$ f\in\mathbf{Q}[x]$](img205.png)
of least positive degree such that
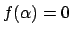
.
The minimal polynomial of 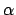 divides any polynomial
divides any polynomial 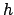 such
that
such
that
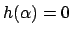 , for the following reason. If
, for the following reason. If
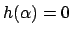 , use
the division algorithm to write
, use
the division algorithm to write 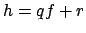 , where
, where
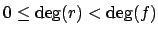 . We have
. We have
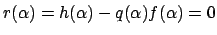 ,
so
,
so 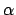 is a root of
is a root of 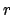 . However,
. However, 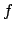 is the polynomial of least
positive degree with root
is the polynomial of least
positive degree with root 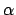 , so
, so 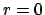 .
.
Lemma 5.1.3
If 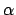 is an algebraic integer, then the minimal polynomial
of
is an algebraic integer, then the minimal polynomial
of 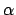 has coefficients in
has coefficients in
 .
.
Proof.
Suppose
![$ f\in\mathbf{Q}[x]$](img205.png)
is the minimal polynomial of
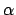
and
![$ g\in\mathbf{Z}[x]$](img212.png)
is a monic integral polynomial such that
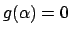
.
As mentioned after the definition of minimal polynomial, we have
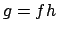
, for some
![$ h\in\mathbf{Q}[x]$](img215.png)
. If
![$ f\not\in\mathbf{Z}[x]$](img216.png)
, then some prime
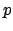
divides the denominator of some coefficient of
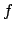
. Let
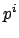
be the
largest power of
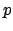
that divides some denominator of some
coefficient
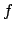
, and likewise let
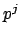
be the largest power of
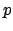
that divides some denominator of a coefficient of
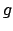
. Then
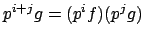
, and if we reduce both sides modulo
, then the
left hand side is
0 but the right hand side is a product of two
nonzero polynomials in
![$ \mathbf{F}_p[x]$](img220.png)
, hence nonzero, a contradiction.

Proposition 5.1.4
An element
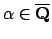 is integral if and only if
is integral if and only if
![$ \mathbf{Z}[\alpha]$](img221.png) is
finitely generated as a
is
finitely generated as a
 -module.
-module.
Proof.
Suppose
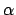
is integral and let
![$ f\in\mathbf{Z}[x]$](img222.png)
be the monic minimal polynomial
of
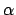
(that
![$ f\in\mathbf{Z}[x]$](img222.png)
is Lemma
5.1.3). Then
![$ \mathbf{Z}[\alpha]$](img221.png)
is generated by
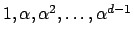
, where
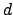
is
the degree of
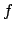
. Conversely, suppose
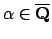
is such that
![$ \mathbf{Z}[\alpha]$](img221.png)
is finitely generated, say by elements
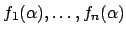
. Let
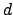
be any integer bigger
than the degree of any
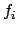
. Then there exist integers
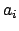
such
that
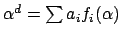
, hence
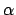
satisfies
the monic polynomial
![$ x^d - \sum a_i f_i(x) \in \mathbf{Z}[x]$](img226.png)
, so
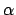
is integral.

The rational number
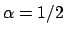 is not integral. Note that
is not integral. Note that
![$ G=\mathbf{Z}[1/2]$](img228.png) is not a finitely generated
is not a finitely generated
 -module, since
-module, since 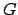 is infinite
and
is infinite
and 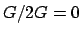 .
.
Proposition 5.1.5
The set
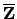 of all algebraic integers is a ring, i.e., the sum and
product of two algebraic integers is again an algebraic integer.
of all algebraic integers is a ring, i.e., the sum and
product of two algebraic integers is again an algebraic integer.
Proof.
Suppose
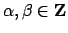
, and let
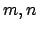
be the degrees of the
minimal polynomials of
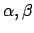
, respectively. Then
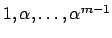
span
![$ \mathbf{Z}[\alpha]$](img221.png)
and
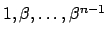
span
![$ \mathbf{Z}[\beta]$](img236.png)
as

-module. Thus
the elements
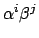
for
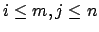
span
![$ \mathbf{Z}[\alpha, \beta]$](img239.png)
. Since
![$ \mathbf{Z}[\alpha + \beta]$](img240.png)
is a submodule of the
finitely-generated module
![$ \mathbf{Z}[\alpha, \beta]$](img239.png)
, it is finitely
generated, so
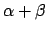
is integral. Likewise,
![$ \mathbf{Z}[\alpha\beta]$](img242.png)
is a submodule of
![$ \mathbf{Z}[\alpha, \beta]$](img239.png)
, so it is also finitely
generated and
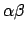
is integral.

Recall that a is a subfield 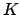 of
of
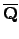 such
that the degree
such
that the degree
![$ [K:\mathbf{Q}] := \dim_\mathbf{Q}(K)$](img244.png) is finite.
is finite.
Definition 5.1.6 (Ring of Integers)
The
of a number field
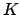
is the ring
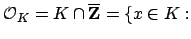
$x$ is an algebraic integer
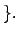
The field
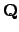 of rational numbers is a number field of degree
of rational numbers is a number field of degree 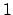 ,
and the ring of integers of
,
and the ring of integers of
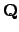 is
is
 . The field
. The field
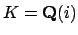 of
Gaussian integers has degree
of
Gaussian integers has degree 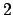 and
and
![$ \O _K = \mathbf{Z}[i]$](img248.png) . The field
. The field
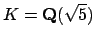 has ring of integers
has ring of integers
![$ \O _K = \mathbf{Z}[(1+\sqrt{5})/2]$](img250.png) .
Note that the Golden ratio
.
Note that the Golden ratio
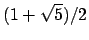 satisfies
satisfies 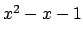 .
According to , the ring of integers of
.
According to , the ring of integers of
![$ K=\mathbf{Q}(\sqrt[3]{9})$](img253.png) is
is
![$ \mathbf{Z}[\sqrt[3]{3}]$](img254.png) , where
, where
![$ \sqrt[3]{3}=\frac{1}{3}(\sqrt[3]{9})^2$](img255.png) .
.
Definition 5.1.7 (Order)
An
in

is any subring
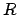
of

such that the
quotient
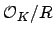
of abelian groups is finite.
(Note that
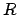
must contain
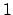
because it is a ring, and for us
every ring has a
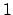
.)
As noted above,
![$ \mathbf{Z}[i]$](img257.png) is the ring of integers of
is the ring of integers of
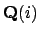 . For every
nonzero integer
. For every
nonzero integer 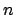 , the subring
, the subring
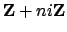 of
of
![$ \mathbf{Z}[i]$](img257.png) is an order.
The subring
is an order.
The subring
 of
of
![$ \mathbf{Z}[i]$](img257.png) is not an order, because
is not an order, because
 does not
have finite index in
does not
have finite index in
![$ \mathbf{Z}[i]$](img257.png) . Also the subgroup
. Also the subgroup
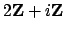 of
of
![$ \mathbf{Z}[i]$](img257.png) is not an order because it is not a ring.
is not an order because it is not a ring.
We will frequently consider orders in practice because they are often
much easier to write down explicitly than  . For example, if
. For example, if
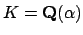 and
and 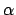 is an algebraic integer, then
is an algebraic integer, then
![$ \mathbf{Z}[\alpha]$](img221.png) is an order in
is an order in  , but frequently
, but frequently
![$ \mathbf{Z}[\alpha]\neq \O _K$](img262.png) .
.
Lemma 5.1.8
Let  be the ring of integers of a number field. Then
be the ring of integers of a number field. Then
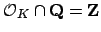 and
and
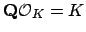 .
.
Proof.
Suppose
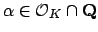
with
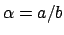
in lowest terms and
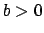
. The monic minimal polynomial of
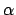
is
![$ bx-a\in\mathbf{Z}[x]$](img268.png)
, so
if
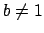
then Lemma
5.1.3 implies that
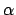
is
not an algebraic integer, a contradiction.
To prove that
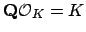 , suppose
, suppose
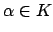 , and let
, and let
![$ f(x)\in\mathbf{Q}[x]$](img271.png) be the minimal monic polynomial of
be the minimal monic polynomial of 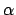 . For any
positive integer
. For any
positive integer 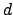 , the minimal monic polynomial of
, the minimal monic polynomial of 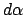 is
is
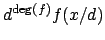 , i.e., the polynomial obtained from
, i.e., the polynomial obtained from 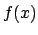 by
multiplying the coefficient of
by
multiplying the coefficient of
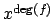 by
by 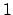 , multiplying the
coefficient of
, multiplying the
coefficient of
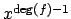 by
by 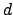 , multiplying the coefficient of
, multiplying the coefficient of
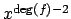 by
by 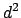 , etc. If
, etc. If 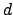 is the least common multiple of
the denominators of the coefficients of
is the least common multiple of
the denominators of the coefficients of 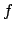 , then the minimal monic
polynomial of
, then the minimal monic
polynomial of 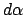 has integer coefficients, so
has integer coefficients, so 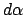 is
integral and
is
integral and
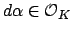 . This proves that
. This proves that
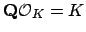 .
.

In the next two sections we will develop some basic properties of
norms and traces, and deduce further properties of rings of integers.
William Stein
2004-05-06
![]() is not integral. Note that
is not integral. Note that
![]() is not a finitely generated
is not a finitely generated
![]() -module, since
-module, since ![]() is infinite
and
is infinite
and ![]() .
.
![]() of
of
![]() such
that the degree
such
that the degree
![]() is finite.
is finite.
![]() of rational numbers is a number field of degree
of rational numbers is a number field of degree ![]() ,
and the ring of integers of
,
and the ring of integers of
![]() is
is
![]() . The field
. The field
![]() of
Gaussian integers has degree
of
Gaussian integers has degree ![]() and
and
![]() . The field
. The field
![]() has ring of integers
has ring of integers
![]() .
Note that the Golden ratio
.
Note that the Golden ratio
![]() satisfies
satisfies ![]() .
According to , the ring of integers of
.
According to , the ring of integers of
![]() is
is
![]() , where
, where
![]() .
.
![]() . For example, if
. For example, if
![]() and
and ![]() is an algebraic integer, then
is an algebraic integer, then
![]() is an order in
is an order in ![]() , but frequently
, but frequently
![]() .
.
![]() , suppose
, suppose
![]() , and let
, and let
![]() be the minimal monic polynomial of
be the minimal monic polynomial of ![]() . For any
positive integer
. For any
positive integer ![]() , the minimal monic polynomial of
, the minimal monic polynomial of ![]() is
is
![]() , i.e., the polynomial obtained from
, i.e., the polynomial obtained from ![]() by
multiplying the coefficient of
by
multiplying the coefficient of
![]() by
by ![]() , multiplying the
coefficient of
, multiplying the
coefficient of
![]() by
by ![]() , multiplying the coefficient of
, multiplying the coefficient of
![]() by
by ![]() , etc. If
, etc. If ![]() is the least common multiple of
the denominators of the coefficients of
is the least common multiple of
the denominators of the coefficients of ![]() , then the minimal monic
polynomial of
, then the minimal monic
polynomial of ![]() has integer coefficients, so
has integer coefficients, so ![]() is
integral and
is
integral and
![]() . This proves that
. This proves that
![]() .
.
![]()